 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
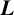 $\boldsymbol {L}$
-FUNCTIONS
$\boldsymbol {L}$
-FUNCTIONS
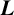 $\boldsymbol {L}$
-VALUE
$\boldsymbol {L}$
-VALUE
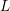 $L$-FUNCTIONS
$L$-FUNCTIONS
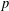 $p$-ADIC
$p$-ADIC 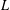 $L$-FUNCTIONS FOR UNITARY GROUPS
$L$-FUNCTIONS FOR UNITARY GROUPS
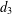 $d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
$d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
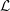 ${\mathcal{L}}$-function of
${\mathcal{L}}$-function of 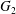 $G_{2}$ and the Rallis–Schiffmann Lift
$G_{2}$ and the Rallis–Schiffmann Lift
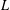 $L$-FUNCTIONS
$L$-FUNCTIONS
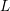 $L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
$L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
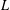 $L$-FUNCTIONS
$L$-FUNCTIONS
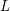 $L$-function on
$L$-function on 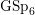 $\text{GSp}_{6}$ for Siegel modular forms
$\text{GSp}_{6}$ for Siegel modular forms