25 results
COMPATIBLE SYSTEMS OF GALOIS REPRESENTATIONS ASSOCIATED TO THE EXCEPTIONAL GROUP
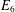 $E_{6}$
$E_{6}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 06 February 2019, e4
-
- Article
-
- You have access
- Open access
- Export citation
Minimally ramified deformations when
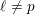 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1-37
- Print publication:
- January 2019
-
- Article
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ARISING FROM HILBERT MODULAR SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 November 2017, e29
-
- Article
-
- You have access
- Open access
- Export citation
On mod
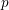 $p$ local-global compatibility for
$p$ local-global compatibility for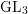 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 25 August 2017, pp. 2215-2286
- Print publication:
- November 2017
-
- Article
- Export citation
SERRE WEIGHTS AND WILD RAMIFICATION IN TWO-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 23 December 2016, e33
-
- Article
-
- You have access
- Open access
- Export citation
The inverse deformation problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1725-1739
- Print publication:
- August 2016
-
- Article
- Export citation
Modular elliptic curves over the field of twelfth roots of unity
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 155-174
-
- Article
-
- You have access
- Export citation
Real-dihedral harmonic Maass forms and CM-values of Hilbert modular functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 1159-1197
- Print publication:
- June 2016
-
- Article
- Export citation
ON THE THETA OPERATOR FOR MODULAR FORMS MODULO PRIME POWERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 321-336
- Print publication:
- 2016
-
- Article
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation
Level 1 Hecke algebras of modular forms modulo
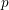 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 397-415
- Print publication:
- March 2015
-
- Article
- Export citation
Big Galois representations and
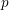 $p$-adic
$p$-adic 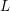 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 13 November 2014, pp. 603-664
- Print publication:
- April 2015
-
- Article
- Export citation
On families of 7- and 11-congruent elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 536-564
-
- Article
-
- You have access
- Export citation
Modularity of nearly ordinary 2-adic residually dihedral Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 1235-1346
- Print publication:
- August 2014
-
- Article
- Export citation
Level-raising and symmetric power functoriality, I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 729-748
- Print publication:
- May 2014
-
- Article
- Export citation
Companion forms in parallel weight one
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 10 May 2013, pp. 903-913
- Print publication:
- June 2013
-
- Article
- Export citation
On admissible tensor products in p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 417-429
- Print publication:
- March 2013
-
- Article
- Export citation
Modularity lifting theorems for Galois representations of unitary type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 18 March 2011, pp. 1022-1058
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
Hilbert modular forms and p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 21 September 2009, pp. 1081-1113
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation

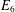
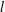
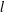
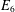
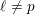
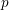
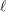
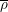

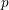
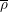
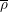
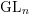
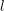
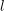
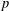
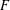
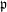
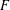
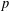
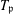
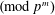
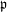
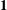
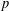
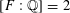
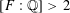
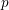
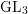
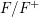
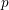
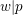
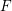
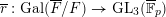
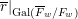

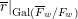
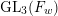
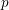



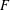
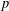
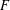
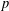
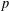
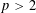
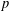
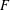
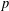
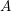
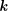

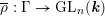
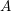
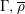
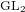



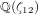
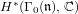
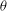
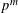
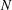
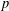
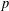
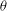
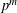
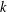
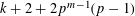
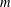
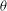
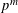
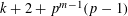
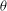
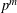
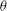
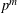
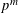
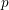

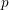
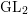
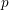
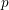
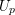
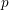
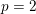
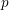
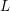
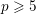
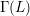
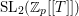
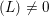
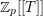
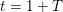
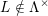
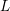
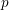
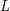
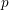
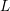

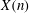
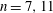


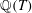
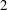
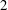
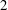
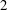
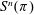

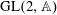
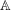
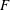
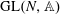
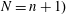
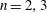
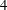
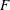

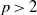
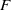
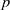
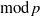
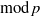
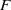
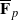 -representation
-representation 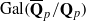 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(