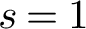 $s=1$
$s=1$
 $\boldsymbol {L}$
-VALUES
$\boldsymbol {L}$
-VALUES
 $\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
$\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
 $p$-ADIC VARIATION OF HEEGNER POINTS
$p$-ADIC VARIATION OF HEEGNER POINTS