 $\boldsymbol {L}$
-FUNCTIONS
$\boldsymbol {L}$
-FUNCTIONS
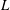 $L$-functions
$L$-functions
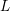 $L$-functions to prime power moduli
$L$-functions to prime power moduli
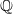 $\mathbb {Q}$
$\mathbb {Q}$