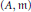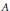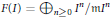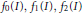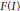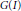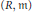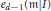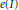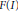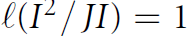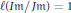15 results
ON THE ASYMPTOTIC BEHAVIOR OF THE VASCONCELOS INVARIANT FOR GRADED MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-15
-
- Article
- Export citation
A sub-functor for Ext and Cohen–Macaulay associated graded modules with bounded multiplicity-II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 30 October 2024, pp. 86-106
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
Derived functors and Hilbert polynomials over regular local rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1137-1147
-
- Article
-
- You have access
- HTML
- Export citation
SYMBOLIC ANALYTIC SPREAD: UPPER BOUNDS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 07 May 2020, pp. 1969-1981
- Print publication:
- November 2021
-
- Article
- Export citation
ON THE CONJECTURE OF VASCONCELOS FOR ARTINIAN ALMOST COMPLETE INTERSECTION MONOMIAL IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 10 December 2019, pp. 263-277
- Print publication:
- September 2021
-
- Article
- Export citation
INTEGRAL CLOSURE OF STRONGLY GOLOD IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 18 July 2019, pp. 204-216
- Print publication:
- March 2021
-
- Article
- Export citation
On Special Fiber Rings of Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 225-242
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
LOCAL COHOMOLOGY OF MULTI-REES ALGEBRAS, JOINT REDUCTION NUMBERS AND PRODUCT OF COMPLETE IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 1-20
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
Minimal Generators of the Defining Ideal of the Rees Algebra Associated with a Rational Plane Parametrization with μ = 2
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 6 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1225-1249
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
The structure of sally modules and Buchsbaumness of associated graded rings
-
- Journal:
- Nagoya Mathematical Journal / Volume 212 / December 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 97-138
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Quasi-socle ideals in Buchsbaum rings
-
- Journal:
- Nagoya Mathematical Journal / Volume 200 / December 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 93-106
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Buchsbaumness in local rings possessing constant first Hilbert coefficients of parameters
-
- Journal:
- Nagoya Mathematical Journal / Volume 199 / September 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 95-105
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
The Hilbert Coefficients of the Fiber Cone and the a-Invariant of the Associated Graded Ring
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 4 / 01 August 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 762-778
- Print publication:
- 01 August 2009
-
- Article
-
- You have access
- Export citation
On Fiber Cones of
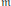 $\text{m}$
-Primary Ideals
$\text{m}$
-Primary Ideals
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 1 / 01 February 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 109-126
- Print publication:
- 01 February 2007
-
- Article
-
- You have access
- Export citation
Rees Algebras of Modules
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 3 / November 2003
- Published online by Cambridge University Press:
- 23 October 2003, pp. 610-646
- Print publication:
- November 2003
-
- Article
- Export citation

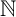

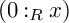
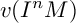
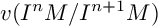
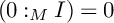
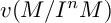

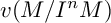
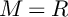
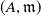
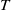
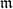
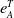
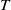
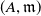
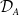
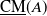
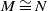
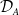
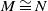
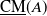
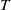
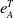
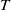
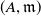
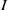
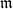
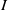
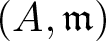
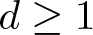
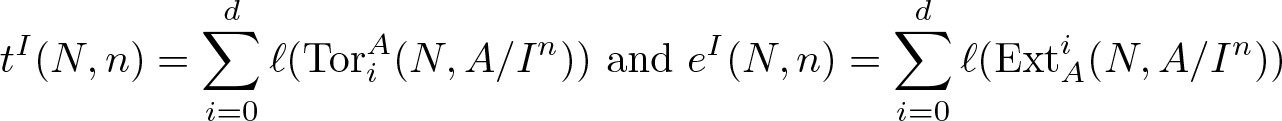
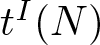
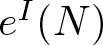
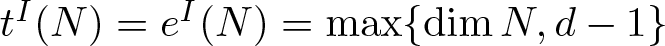
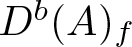


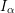
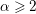
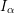
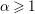
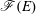
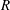
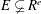
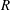
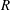
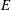
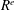
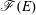
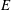
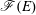
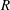
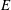
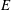
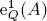 of
of 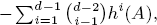 where
where 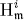 of
of