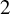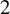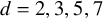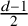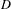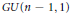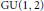22 results
Stability conditions for line bundles on nodal curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic coverings of genus
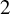 $2$ curves of Sophie Germain type
$2$ curves of Sophie Germain type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 May 2024, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hodge bundle, the universal 0-section, and the log Chow ring of the moduli space of curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 306-354
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOUNDARY OF THE p-RANK
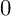 $0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Normalization of Closed Ekedahl—Oort Strata
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 572-587
- Print publication:
- 01 September 2018
-
- Article
-
- You have access
- Export citation
A MODULI INTERPRETATION FOR THE NON-SPLIT CARTAN MODULAR CURVE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 411-434
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Level structures on abelian varieties and Vojta’s conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 373-394
- Print publication:
- February 2017
-
- Article
- Export citation
Abelian Surfaces with an Automorphism and Quaternionic Multiplication
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 1 / 01 February 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-43
- Print publication:
- 01 February 2016
-
- Article
-
- You have access
- Export citation
THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 15 December 2014, pp. 693-710
- Print publication:
- October 2016
-
- Article
- Export citation
Congruence Relations for Shimura Varieties Associated with GU(n–1, 1)
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 6 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1305-1326
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Logarithmic abelian varieties, III: Logarithmic elliptic curves and modular curves
-
- Journal:
- Nagoya Mathematical Journal / Volume 210 / June 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 59-81
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
The Supersingular Locus of the Shimura Variety for GU(1, s)
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 3 / 01 June 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 668-720
- Print publication:
- 01 June 2010
-
- Article
-
- You have access
- Export citation
Supersingular Kottwitz–Rapoport strata and Deligne–Lusztig varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 August 2009, pp. 357-390
- Print publication:
- April 2010
-
- Article
- Export citation
Logarithmic Abelian Varieties
-
- Journal:
- Nagoya Mathematical Journal / Volume 189 / 2008
- Published online by Cambridge University Press:
- 11 January 2016, pp. 63-138
- Print publication:
- 2008
-
- Article
-
- You have access
- Export citation
INTERSECTION THEORY OF TOROIDAL COMPACTIFICATIONS OF ${\cal A}_4$
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 31 May 2006, pp. 396-400
- Print publication:
- June 2006
-
- Article
- Export citation
CONGRUENCE RELATIONS FOR SHIMURA VARIETIES ASSOCIATED TO SOME UNITARY GROUPS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 5 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 07 December 2005, pp. 229-261
- Print publication:
- April 2006
-
- Article
- Export citation
on the hilbert–blumenthal moduli problem
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 4 / Issue 4 / October 2005
- Published online by Cambridge University Press:
- 29 July 2005, pp. 653-683
- Print publication:
- October 2005
-
- Article
- Export citation
Some Calabi–Yau threefolds with obstructed deformations over the Witt vectors
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 6 / November 2004
- Published online by Cambridge University Press:
- 15 October 2004, pp. 1579-1592
- Print publication:
- November 2004
-
- Article
-
- You have access
- Export citation
The nef cone of toroidal compactifications of ${\cal A}_4$
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 88 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 14 April 2004, pp. 659-704
- Print publication:
- May 2004
-
- Article
- Export citation
Cohomology of Complex Torus Bundles Associated to Cocycles
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 4 / 01 August 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 839-855
- Print publication:
- 01 August 2003
-
- Article
-
- You have access
- Export citation