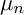 $\mu _{n}$
-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
$\mu _{n}$
-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
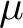 $\mu $
-STABILIZERS IN ACF
$\mu $
-STABILIZERS IN ACF