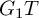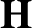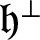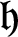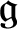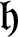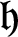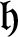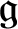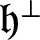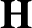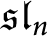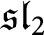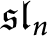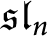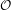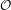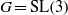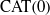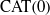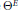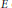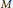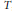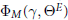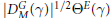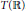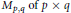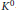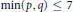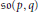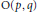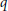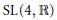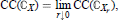16 results
AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
A HECKE ACTION ON
 $G_1T$-MODULES
$G_1T$-MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1125-1167
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Annihilator varieties of distinguished modules of reductive Lie algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e52
-
- Article
-
- You have access
- Open access
- Export citation
Categorification via blocks of modular representations for
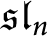 $\mathfrak {sl}_n$
$\mathfrak {sl}_n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 19 May 2020, pp. 1095-1123
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
PERVERSE MOTIVES AND GRADED DERIVED CATEGORY
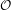 ${\mathcal{O}}$
${\mathcal{O}}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2016, pp. 347-395
- Print publication:
- April 2018
-
- Article
- Export citation
Buildings, spiders, and geometric Satake
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1871-1912
- Print publication:
- November 2013
-
- Article
- Export citation
Duality for nonlinear simply laced groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 931-965
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Decomposition of Splitting Invariants in Split Real Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 5 / 18 October 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1083-1106
- Print publication:
- 18 October 2011
-
- Article
-
- You have access
- Export citation
Stable Discrete Series Characters at Singular Elements
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1375-1382
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
Leading-term cycles of Harish-Chandra modules and partial orders on components of the Springer fiber
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 2 / March 2007
- Published online by Cambridge University Press:
- 26 March 2007, pp. 515-540
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Derived functor modules arising as large irreducible constituents of degenerate principal series
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 19 January 2007, pp. 222-256
- Print publication:
- January 2007
-
- Article
-
- You have access
- Export citation
On the representations of Sp(p, q) and SO*(2n) unitarily induced from derived functor modules
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1059-1096
- Print publication:
- July 2004
-
- Article
-
- You have access
- Export citation
Structure of Modules Induced from Simple Modules with Minimal Annihilator
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 2 / 01 April 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 293-309
- Print publication:
- 01 April 2004
-
- Article
-
- You have access
- Export citation
The Closure Ordering of Nilpotent Orbits of the Complex Symmetric Pair (SOp+q, SOp × SOq)
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 6 / 01 December 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1155-1190
- Print publication:
- 01 December 2003
-
- Article
-
- You have access
- Export citation
On Some
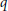 $q$-Analogs of a Theorem of Kostant-Rallis
$q$-Analogs of a Theorem of Kostant-Rallis
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 2 / 01 April 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 438-448
- Print publication:
- 01 April 2000
-
- Article
-
- You have access
- Export citation
Characteristic Cycles in Hermitian Symmetric Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 3 / 01 June 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-467
- Print publication:
- 01 June 1997
-
- Article
-
- You have access
- Export citation