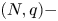 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$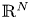 with new exponential growth conditions
with new exponential growth conditions
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
 $n$ INTEGERS
$n$ INTEGERS
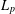 $L_{p}$-HARDY INEQUALITY
$L_{p}$-HARDY INEQUALITY