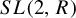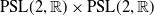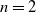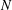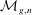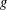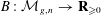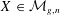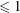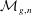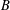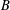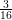31 results
The coarse geometry of hexagon decomposition graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasidiagonals in strata of translation surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Period realization of meromorphic differentials with prescribed invariants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective count of square-tiled surfaces with prescribed real and imaginary foliations in connected components of strata
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 649-662
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weyl chamber length compactification of the
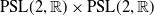 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 11-33
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
Nonvarying, affine and extremal geometry of strata of differentials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 361-371
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the gradient flow of renormalized volume to convex cores with totally geodesic boundary
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 830-859
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric filling curves on punctured surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 383-400
- Print publication:
- May 2023
-
- Article
- Export citation
Dilogarithm identities after Bridgeman
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 03 March 2022, pp. 1-23
- Print publication:
- January 2023
-
- Article
- Export citation
Gaps of saddle connection directions for some branched covers of tori
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 03 August 2021, pp. 3191-3245
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SIMPLE SEPARATING SYSTOLE FOR HYPERBOLIC SURFACES OF LARGE GENUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 2205-2214
- Print publication:
- November 2022
-
- Article
- Export citation
RECURSION FOR MASUR-VEECH VOLUMES OF MODULI SPACES OF QUADRATIC DIFFERENTIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1471-1476
- Print publication:
- July 2022
-
- Article
- Export citation
ENUMERATION OF MEANDERS AND MASUR–VEECH VOLUMES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 23 March 2020, e4
-
- Article
-
- You have access
- Open access
- Export citation
SQUARE-INTEGRABILITY OF THE MIRZAKHANI FUNCTION AND STATISTICS OF SIMPLE CLOSED GEODESICS ON HYPERBOLIC SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 February 2020, e9
-
- Article
-
- You have access
- Open access
- Export citation
Short closed geodesics with self-intersections
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 623-638
- Print publication:
- November 2020
-
- Article
- Export citation
On Selberg’s eigenvalue conjecture for moduli spaces of abelian differentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 30 October 2019, pp. 2354-2398
- Print publication:
- December 2019
-
- Article
- Export citation
Green Function and Self-adjoint Laplacians on Polyhedral Surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 02 July 2019, pp. 1324-1351
- Print publication:
- October 2020
-
- Article
- Export citation
An origami of genus 3 with arithmetic Kontsevich–Zorich monodromy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 08 March 2019, pp. 19-30
- Print publication:
- July 2020
-
- Article
- Export citation
Cascades in the dynamics of affine interval exchange transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 2073-2097
- Print publication:
- August 2020
-
- Article
- Export citation
NONDECREASABLE AND WEAKLY NONDECREASABLE DILATATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 420-434
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation