 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
 $\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
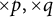 $\times p,\times q$ conjecture
$\times p,\times q$ conjecture
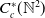 $C_c^{*}(\mathbb{N}^2)$
$C_c^{*}(\mathbb{N}^2)$
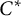 $C^*$-algebras associated with minimal shift spaces
$C^*$-algebras associated with minimal shift spaces
 $^*$-algebras
$^*$-algebras
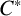 $C^*$-ALGEBRAS OF SELF-SIMILAR ACTION OF GROUPOIDS ON ROW-FINITE DIRECTED GRAPHS
$C^*$-ALGEBRAS OF SELF-SIMILAR ACTION OF GROUPOIDS ON ROW-FINITE DIRECTED GRAPHS
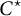 $C^\star $-algebras
$C^\star $-algebras