16 results
On weighted-blowup formulae of genus zero orbifold Gromov–Witten invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1833-1871
- Print publication:
- September 2023
-
- Article
- Export citation
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Open-closed Gromov-Witten invariants of 3-dimensional Calabi-Yau smooth toric DM stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 July 2022, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLUTIONS OF THE tt*-TODA EQUATIONS AND QUANTUM COHOMOLOGY OF MINUSCULE FLAG MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 990-1004
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasimaps to GIT fibre bundles and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 August 2021, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The genus-one global mirror theorem for the quintic
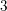 $3$-fold
$3$-fold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 30 April 2019, pp. 995-1024
- Print publication:
- May 2019
-
- Article
- Export citation
VARIATIONS OF BPS STRUCTURE AND A LARGE RANK LIMIT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2019, pp. 103-135
- Print publication:
- January 2021
-
- Article
- Export citation
POTENTIALS OF A FROBENIUS-LIKE STRUCTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 681-693
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF A GLOBAL NEIGHBOURHOOD
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 717-726
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
Pseudoholomorphic tori in the Kodaira–Thurston manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 2212-2250
- Print publication:
- December 2015
-
- Article
- Export citation
Quantum reconstruction for Fano bundles on projective space
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-28
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Computing certain Gromov-Witten invariants of the crepant resolution of ℙ(1, 3, 4, 4)
-
- Journal:
- Nagoya Mathematical Journal / Volume 201 / March 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-22
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Rigid subsets of symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 773-826
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Holomorphic 2-Forms and Vanishing Theorems for Gromov–Witten Invariants
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 87-94
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation
Quantum cohomology of the Grassmannian and alternate Thom–Sebastiani
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 221-246
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
The Chen–Ruan Cohomology of Weighted Projective Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 981-1007
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation