 ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
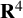 $\mathbf {R}^{4}$
$\mathbf {R}^{4}$
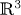
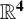 $\boldsymbol {{\mathbb {R}}^{4}}$
$\boldsymbol {{\mathbb {R}}^{4}}$
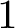 $1$ MINIMAL k-NOIDS AND SADDLE TOWERS IN
$1$ MINIMAL k-NOIDS AND SADDLE TOWERS IN 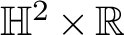 $\mathbb {H}^2\times \mathbb {R}$
$\mathbb {H}^2\times \mathbb {R}$