We provide upper and lower bounds for the mean 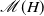 $\mathscr{M}(H)$
of
$\mathscr{M}(H)$
of 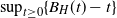 $\sup_{t\geq 0} \{B_H(t) - t\}$
, with
$\sup_{t\geq 0} \{B_H(t) - t\}$
, with 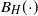 $B_H(\!\cdot\!)$
a zero-mean, variance-normalized version of fractional Brownian motion with Hurst parameter
$B_H(\!\cdot\!)$
a zero-mean, variance-normalized version of fractional Brownian motion with Hurst parameter 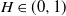 $H\in(0,1)$
. We find bounds in (semi-) closed form, distinguishing between
$H\in(0,1)$
. We find bounds in (semi-) closed form, distinguishing between 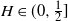 $H\in(0,\frac{1}{2}]$
and
$H\in(0,\frac{1}{2}]$
and 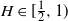 $H\in[\frac{1}{2},1)$
, where in the former regime a numerical procedure is presented that drastically reduces the upper bound. For
$H\in[\frac{1}{2},1)$
, where in the former regime a numerical procedure is presented that drastically reduces the upper bound. For 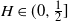 $H\in(0,\frac{1}{2}]$
, the ratio between the upper and lower bound is bounded, whereas for
$H\in(0,\frac{1}{2}]$
, the ratio between the upper and lower bound is bounded, whereas for 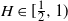 $H\in[\frac{1}{2},1)$
the derived upper and lower bound have a strongly similar shape. We also derive a new upper bound for the mean of
$H\in[\frac{1}{2},1)$
the derived upper and lower bound have a strongly similar shape. We also derive a new upper bound for the mean of 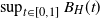 $\sup_{t\in[0,1]} B_H(t)$
,
$\sup_{t\in[0,1]} B_H(t)$
, 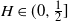 $H\in(0,\frac{1}{2}]$
, which is tight around
$H\in(0,\frac{1}{2}]$
, which is tight around 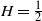 $H=\frac{1}{2}$
.
$H=\frac{1}{2}$
.
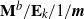 $\mathbf{M}^{b}/\mathbf{E}_{k}/1/\textbf{m}$
,
$\mathbf{M}^{b}/\mathbf{E}_{k}/1/\textbf{m}$
, 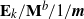 $\mathbf{E}_{k}/\mathbf{M}^{b}/1/\textbf{m}$
, and related queues
$\mathbf{E}_{k}/\mathbf{M}^{b}/1/\textbf{m}$
, and related queues