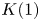 $K(1)$-local
$K(1)$-local 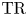 $\mathrm {TR}$
$\mathrm {TR}$
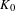 $K_{0}$-GROUPS AND CHOW GROUPS WITH MODULUS
$K_{0}$-GROUPS AND CHOW GROUPS WITH MODULUS
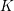 $K$-theory revisited
$K$-theory revisited
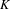 $K$-THEORY OF MONOID ALGEBRAS AND A QUESTION OF GUBELADZE
$K$-THEORY OF MONOID ALGEBRAS AND A QUESTION OF GUBELADZE
 $\infty$-categories and the Theorem of the Heart
$\infty$-categories and the Theorem of the Heart
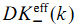
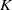 $K$-GROUPS
$K$-GROUPS