Refine search
Actions for selected content:
43 results
Large and moderate deviations for Gaussian neural networks
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-20
-
- Article
- Export citation
Global existence and some qualitative properties of weak solutions for a class of pseudo-parabolic equations with a logarithmic nonlinearity in whole
 $\mathbb{R}^{N}$
$\mathbb{R}^{N}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-44
-
- Article
- Export citation
A free boundary problem of competition-diffusion system with Dirichlet boundary condition
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-20
-
- Article
- Export citation
A Comparison of Game Theory and Learning Theory
-
- Journal:
- Psychometrika / Volume 21 / Issue 3 / September 1956
- Published online by Cambridge University Press:
- 01 January 2025, pp. 267-272
-
- Article
- Export citation
Solvability of Hessian quotient equations in exterior domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 December 2023, pp. 118-148
- Print publication:
- February 2025
-
- Article
- Export citation
Nonlinear Beltrami equation: lower estimates of Schwarz lemma’s type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 533-543
- Print publication:
- September 2024
-
- Article
- Export citation
Branching Brownian motion in a periodic environment and uniqueness of pulsating traveling waves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 09 November 2022, pp. 510-548
- Print publication:
- June 2023
-
- Article
- Export citation
Large-scale behavior of a particle system with mean-field interaction: Traveling wave solutions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 September 2022, pp. 245-274
- Print publication:
- March 2023
-
- Article
- Export citation
Existence of hypercylinder expanders of the inverse mean curvature flow
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 05 July 2021, pp. 543-551
- Print publication:
- September 2022
-
- Article
- Export citation
Autonomous and non-autonomous unbounded attractors under perturbations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 877-903
- Print publication:
- August 2019
-
- Article
- Export citation
A NEW STOPPING PROBLEM AND THE CRITICAL EXERCISE PRICE FOR AMERICAN FRACTIONAL LOOKBACK OPTION IN A SPECIAL MIXED JUMP-DIFFUSION MODEL
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 September 2018, pp. 27-52
-
- Article
- Export citation
Kesten's bound for subexponential densities on the real line and its multi-dimensional analogues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 373-395
- Print publication:
- June 2018
-
- Article
- Export citation
The Asymptotics of the Higher Dimensional Reidemeister Torsion for Exceptional Surgeries Along Twist Knots
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 211-224
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
Integrable Properties of a Variant of the Discrete Hungry Toda Equations and Their Relationship to Eigenpairs of Band Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 785-798
- Print publication:
- November 2017
-
- Article
- Export citation
Asymptotic behaviour and symmetry of positive solutions to nonlinear elliptic equations in a half-space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1243-1263
- Print publication:
- December 2016
-
- Article
- Export citation
Existence and Asymptotic Behavior of Positive Solutions for Variable Exponent Elliptic Systems
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 21 December 2015, pp. 19-36
- Print publication:
- February 2016
-
- Article
- Export citation
A hyperbolic model of chemotaxison a network: a numerical study
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 231-258
- Print publication:
- January 2014
-
- Article
- Export citation
Asymptotics and Uniqueness of Travelling Waves for Non-Monotone Delayed Systems on 2D Lattices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 659-672
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
Numerical Approximations of the Dynamical System Generated byBurgers’ Equation with Neumann–Dirichlet Boundary Conditions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 5 / September 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 1465-1492
- Print publication:
- September 2013
-
- Article
- Export citation
Asymptotic Behavior of Solutions to Diffusion Problems withRobin and Free Boundary Conditions
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 3 / 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 18-32
- Print publication:
- 2013
-
- Article
- Export citation


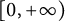


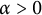

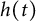
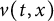
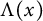
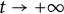


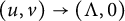
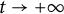


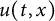

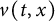
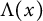

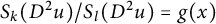
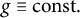
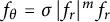

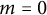
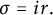
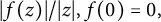
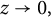
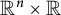
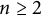
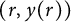
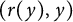
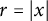
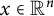
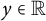
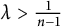
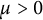
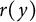
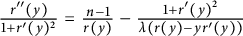
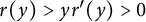
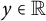
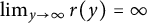
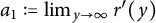
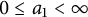
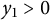
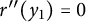
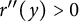
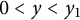
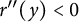
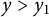
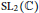
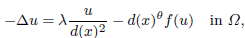
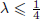 ,
, 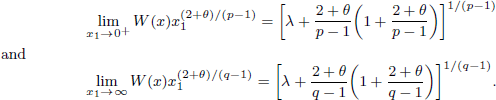
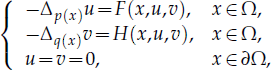
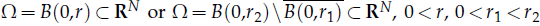 are constants.
are constants. 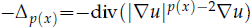 is called
is called 
