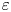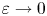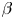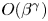33 results
Control of the boundary layer on compressor blade suction surfaces with the momentum jet
-
- Journal:
- The Aeronautical Journal / Volume 127 / Issue 1316 / October 2023
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1793-1816
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Viscous Shear Flow
-
- Book:
- A Guide to Fluid Mechanics
- Published online:
- 16 March 2023
- Print publication:
- 23 March 2023, pp 128-190
-
- Chapter
- Export citation

A Guide to Fluid Mechanics
-
- Published online:
- 16 March 2023
- Print publication:
- 23 March 2023
5 - The Energy Equation and a Discussion on Diffusion and Advection
-
- Book:
- A Student's Guide to the Navier-Stokes Equations
- Published online:
- 10 March 2023
- Print publication:
- 09 February 2023, pp 124-181
-
- Chapter
- Export citation
Dirichlet vs Neumann
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1063-1074
-
- Article
- Export citation
Thermoacoustic effects on the propagation of non-planar sound in a circular duct
-
- Journal:
- Journal of Fluid Mechanics / Volume 945 / 25 August 2022
- Published online by Cambridge University Press:
- 22 July 2022, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Constraints on the wall layer in turbulent pipe flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 944 / 10 August 2022
- Published online by Cambridge University Press:
- 01 July 2022, A32
-
- Article
- Export citation
Boundary layer of Hsieh's equation with conservative nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1167-1197
- Print publication:
- August 2023
-
- Article
- Export citation
Physical aspects of CMAS particle dynamics and deposition in turboshaft engines
-
- Journal:
- Journal of Materials Research / Volume 35 / Issue 17 / 14 September 2020
- Published online by Cambridge University Press:
- 14 September 2020, pp. 2249-2259
- Print publication:
- 14 September 2020
-
- Article
- Export citation
Ferrofluid thin films for aerofoil lift enhancement and delaying flow separation
-
- Journal:
- The Aeronautical Journal / Volume 124 / Issue 1282 / December 2020
- Published online by Cambridge University Press:
- 18 August 2020, pp. 1865-1878
-
- Article
- Export citation
Chapter 4 - Flow Dynamics in Rivers
-
- Book:
- River Dynamics
- Published online:
- 30 April 2020
- Print publication:
- 07 May 2020, pp 72-96
-
- Chapter
- Export citation
2 - The Wind and Its Characteristics
-
- Book:
- Wind Turbines
- Published online:
- 08 February 2020
- Print publication:
- 20 February 2020, pp 13-33
-
- Chapter
- Export citation
Temporal Variation of Atmospheric Fossil and Modern CO2 Excess at a Central European Rural Tower Station between 2008 and 2014
-
- Journal:
- Radiocarbon / Volume 60 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 19 September 2018, pp. 1285-1299
- Print publication:
- October 2018
-
- Article
- Export citation
Interaction of a Vortex Induced by a Rotating Cylinder with a Plane
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 599-619
- Print publication:
- September 2017
-
- Article
- Export citation
On the Generation of Instability Tollmien-Schlichting Waves by Free-Stream Turbulence
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 429-438
- Print publication:
- April 2017
-
- Article
- Export citation
Numerical Study of Nanosecond Pulsed Plasma Actuator in Laminar Flat Plate Boundary Layer
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1424-1442
- Print publication:
- November 2016
-
- Article
- Export citation
A Mixed Analytical/Numerical Method for Velocity and Heat Transfer of Laminar Power-Law Fluids
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 315-336
- Print publication:
- August 2016
-
- Article
- Export citation
A Novel Technique for Constructing Difference Schemes for Systems of Singularly Perturbed Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1287-1301
- Print publication:
- May 2016
-
- Article
- Export citation
Fitted Mesh Method for a Class of Singularly Perturbed Differential-Difference Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 496-514
- Print publication:
- November 2015
-
- Article
- Export citation
Multiscale Basis Functions for Singular Perturbation on Adaptively Graded Meshes
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 6 / Issue 5 / October 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 604-614
- Print publication:
- October 2014
-
- Article
- Export citation