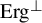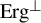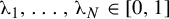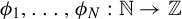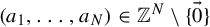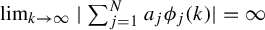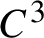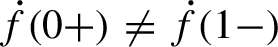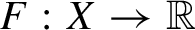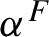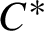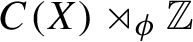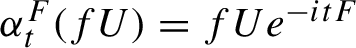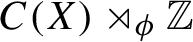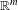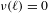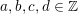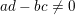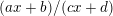38 results
12 - Entropy of Ergodic Processes
- from Part II - Lossless Data Compression
-
- Book:
- Information Theory
- Published online:
- 09 January 2025
- Print publication:
- 02 January 2025, pp 231-244
-
- Chapter
- Export citation
Joining properties of automorphisms disjoint with all ergodic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric properties of disintegration of measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Multiplicity of topological systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 05 February 2024, pp. 2832-2858
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
On the ergodicity of unitary frame flows on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 2143-2172
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Strongly mixing systems are almost strongly mixing of all orders
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 13 September 2023, pp. 1489-1530
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A QUANTITATIVE EVALUATION OF LAGRANGIAN COHERENT STRUCTURE DETECTION METHODS BASED ON COMPUTATIONAL AND EXPERIMENTAL LIMITATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 173-174
- Print publication:
- February 2023
-
- Article
-
- You have access
- HTML
- Export citation
Mixing and rigidity along asymptotically linearly independent sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 3506-3537
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The natural extension of the random beta-transformation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 3861-3896
- Print publication:
- November 2023
-
- Article
- Export citation
Distal systems in topological dynamics and ergodic theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 2651-2672
- Print publication:
- August 2023
-
- Article
- Export citation
An uncountable Furstenberg–Zimmer structure theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 2404-2436
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An uncountable Moore–Schmidt theorem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 2376-2403
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SZEMERÉDI’S THEOREM: AN EXPLORATION OF IMPURITY, EXPLANATION, AND CONTENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 700-739
- Print publication:
- September 2023
-
- Article
- Export citation
A piecewise smooth Fermi–Ulam pingpong with potential
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1847-1870
- Print publication:
- May 2022
-
- Article
- Export citation
KMS states on the crossed product C^* -algebra of a homeomorphism
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 1373-1414
- Print publication:
- April 2022
-
- Article
- Export citation
LOSIK CLASSES FOR CODIMENSION-ONE FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1391-1419
- Print publication:
- July 2022
-
- Article
- Export citation
2 - Algorithmic randomness in ergodic theory
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 40-57
-
- Chapter
- Export citation
Weak ergodic averages over dilated measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 606-621
- Print publication:
- February 2021
-
- Article
- Export citation
Non-trivial matrix actions preserve normality for continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 274-293
- Print publication:
- February 2017
-
- Article
- Export citation
ON ASPECTS OF NUMERICAL ERGODIC THEORY: STABILITY OF ULAM’S METHOD, COMPUTING OSELEDETS SUBSPACES AND OPTIMAL MIXING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 165-166
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation