Let  $T$ be a contraction on a complex, separable, infinite dimensional Hilbert space and let
$T$ be a contraction on a complex, separable, infinite dimensional Hilbert space and let 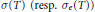 $\sigma (T)\,(\text{resp}\text{.}\,{{\sigma }_{e}}(T))$ be its spectrum (resp. essential spectrum). We assume that
$\sigma (T)\,(\text{resp}\text{.}\,{{\sigma }_{e}}(T))$ be its spectrum (resp. essential spectrum). We assume that  $T$ is an essentially isometric operator; that is,
$T$ is an essentially isometric operator; that is, 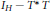 ${{I}_{H}}\,-\,T*T$ is compact. We show that if
${{I}_{H}}\,-\,T*T$ is compact. We show that if 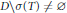 $D\backslash \sigma (T)\,\ne \,\varnothing $, then for every
$D\backslash \sigma (T)\,\ne \,\varnothing $, then for every 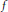 $f$ from the disc-algebra
$f$ from the disc-algebra
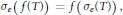 $${{\sigma }_{e}}\left( f\left( T \right) \right)\,=\,f\left( {{\sigma }_{e}}\left( T \right) \right),$$
$${{\sigma }_{e}}\left( f\left( T \right) \right)\,=\,f\left( {{\sigma }_{e}}\left( T \right) \right),$$
where 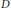 $D$ is the open unit disc. In addition, if
$D$ is the open unit disc. In addition, if  $T$ lies in the class
$T$ lies in the class 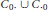 ${{C}_{0}}.\,\bigcup \,C{{.}_{0}}$, then
${{C}_{0}}.\,\bigcup \,C{{.}_{0}}$, then
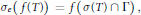 $${{\sigma }_{e}}\left( f\left( T \right) \right)\,=\,f\left( \sigma \left( T \right)\,\bigcap \,\Gamma \right),$$
$${{\sigma }_{e}}\left( f\left( T \right) \right)\,=\,f\left( \sigma \left( T \right)\,\bigcap \,\Gamma \right),$$
where  $\Gamma $ is the unit circle. Some related problems are also discussed.
$\Gamma $ is the unit circle. Some related problems are also discussed.
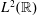 $L^{2}(\mathbb{R})$
$L^{2}(\mathbb{R})$