Heavy particles suspended in turbulent flow possess inertia and are ejected from violent vortical structures by centrifugal forces. Once piled up along particle paths, this small-scale mechanism leads to an effective large-scale drift. This phenomenon, known as ‘turbophoresis’, causes particles to leave highly turbulent regions and migrate towards calmer regions, explaining why particles transported by non-homogeneous flows tend to concentrate near the minima of turbulent kinetic energy. It is demonstrated here that turbophoretic effects are just as crucial in statistically homogeneous flows. Although the average turbulent activity is uniform, instantaneous spatial fluctuations are responsible for inertial-range inhomogeneities in the particle distribution. Direct numerical simulations are used to probe particle accelerations, specifically how they correlate to local turbulent activity, yielding an effective coarse-grained dynamics that accounts for particle detachment from the fluid and ejection from excited regions through a space- and time-dependent non-Fickian diffusion. This leads to cast fluctuations in particle distributions in terms of a scale-dependent Péclet number ${\textit {Pe}}_\ell$, which measures the importance of turbulent advection compared with inertial turbophoresis at a given scale $\ell$. Multifractal statistics of energy dissipation indicate that $ {\textit {Pe}}_\ell \sim \ell ^\delta /\tau _{p}$ with $\delta \approx 0.84$. Numerical simulations support this behaviour and emphasise the relevance of the turbophoretic Péclet number in characterising how particle distributions, including their radial distribution function, depends on $\ell$. This approach also explains the presence of voids with inertial-range sizes, and the fact that their volumes have a non-trivial distribution with a power-law tail $p(\mathcal {V}) \propto \mathcal {V}^{-\alpha }$, with an exponent $\alpha$ that tends to 2 as ${\textit {Pe}}_\ell \to 0$.

This study investigates the influence of surface wave characteristics, specifically wave steepness and directional spreading, on intermittency in deep-water gravity wave turbulence through long-term numerical simulations of three-dimensional potential fully nonlinear periodic gravity waves. We conducted this investigation by estimating the scaling exponent of the surface elevation under different sea state conditions. With our numerical methods, we were able to evaluate the scaling exponents of the structure-function up to 12th order. The observed increased intermittency in directionally narrower sea states and in higher steepness conditions aligns with known effects of quasi-resonant wave–wave interactions and wave breaking. Comparative analyses reveal that both the conventional She–Leveque model and the multifractal models, also used to represent intermittency in wave turbulence of a different nature, exhibit a strong correlation in this study. This observation underscores the universality of intermittency phenomena within wave turbulence.

Turbulent entrainment at the turbulent/non-turbulent interface (TNTI) plays an important role in understanding the turbulent diffusion. While entrainment in fully developed canonical turbulent flows has been extensively studied, the evolution of entrainment in spatially developing flows remains poorly understood. In this work, characteristics of entrainment and the effect of vortices on entrainment of the shear layer separated from a wall-mounted fence are studied by the experiment in a water channel. The shedding vortex experiences a series of stages, including generation, growth, deformation and breakdown into smaller vortices. With the development of the flow, entrainment varies correspondingly. The prograde vortex near the TNTI is found to suppress entrainment but have little effect on the detrainment process, while the retrograde vortex promotes entrainment and suppresses detrainment as well. Consequently, the local entrainment velocity is decreased by the prograde vortex and increased more significantly by the retrograde vortex. Along the streamwise direction, the time-mean entrainment velocity is smallest where the prograde vortex is strongest in the vortex deformation stage. However, the largest time-mean entrainment velocity is located where the enstrophy gradient near the TNTI is greatest after reattachment, rather than where the retrograde vortex is strongest shortly after the breakdown of the shedding vortex, because the scarcity of retrograde vortices in the vicinity of the TNTI makes their long-time cumulative contribution not as significant as their local enhancement. The present study reveals how entrainment evolves in the separated and reattaching flow, and improves our understanding of the effect of vortices on entrainment.

Velocity gradient tensor, $A_{ij}\equiv \partial u_i/\partial x_j$, in a turbulence flow field is modelled by separating the treatment of intermittent magnitude ($A = \sqrt {A_{ij}A_{ij}}$) from that of the more universal normalised velocity gradient tensor, $b_{ij} \equiv A_{ij}/A$. The boundedness and compactness of the $b_{ij}$-space along with its universal dynamics allow for the development of models that are reasonably insensitive to Reynolds number. The near-lognormality of the magnitude $A$ is then exploited to derive a model based on a modified Ornstein–Uhlenbeck process. These models are developed using data-driven strategies employing high-fidelity forced isotropic turbulence data sets. A posteriori model results agree well with direct numerical simulation data over a wide range of velocity-gradient features and Reynolds numbers.

A spatially developing flat-plate boundary layer free from and two-way coupled with inertial solid particles is simulated to investigate the interaction between particles and the turbulent/non-turbulent interface. Particle Stokes numbers based on the outer scale are $St=2$ (low), 11 (moderate) and 53 (high). The Eulerian–Lagrangian point-particle approach is deployed for the simulation of particle-laden flow. The outer edge of the turbulent/non-turbulent interface layer is detected as an iso-surface of vorticity magnitude. Results show that the particles tend to accumulate below the interface due to the centrifugal effect of large-scale vortices in the outer region of wall turbulence and the combined barrier effect of potential flow. Consequently, the conditionally averaged fluid velocity and vorticity vary more significantly across the interface through momentum exchange and the feedback of force in the enstrophy transport. The large-scale structures in the outer layer of turbulence become smoother and less inclined in particle-laden flow due to the modulation of turbulence by the inertial particles. As a result, the geometric features of the interface layer are changed, namely, the spatial undulation increases, the fractal dimension decreases and the thickness becomes thinner in particle-laden flow as compared with unladen case. These effects become more pronounced as particle inertia increases.

The progressive destabilisation of the incompressible flow in a cubical cavity driven by a constant shear stress is investigated numerically. To that end, one of the square faces of the cube is subjected to a constant shear stress parallel to two opposite edges of that face. The three-dimensional steady basic flow loses its mirror symmetry through a supercritical pitchfork bifurcation leading to a pair of steady stable non-symmetric flow states that are antisymmetric to each other. Upon increase of the strength of the driving, these non-symmetric equilibria become unstable via a Hopf bifurcation resulting in two limit cycles. The bifurcations are investigated using classical linear stability analyses as well as nonlinear simulations. Upon a further increase of the driving shear stress, the limit cycles destabilise through bursts triggering a complex interplay between the unstable equilibria. The transition to turbulence resembles the Pomeau–Manneville scenario.

Direct numerical simulations up to Reλ = 1445 show that the scaling exponents for the enstrophy and the dissipation rate extrema are different and depend on the Reynolds number. A similar Reynolds number dependence of the scaling exponents is observed for the moments of the dissipation rate, but not for the moments of the enstrophy. Significant changes in the exponents occur at approximately Reλ ≈ 250, where Reλ is the Taylor based Reynolds number, which coincides with structural changes in the flow, in particular the development of large-scale shear layers. A model for the probability density functions (PDFs) of the enstrophy and dissipate rate is presented, which is an extension of our existing model (Proc. R. Soc. A, vol. 476, 2020, p. 20200591) and is based on the mentioned development of large-scale layer regions within the flow. This model is able to capture the observed Reynolds number dependencies of the scaling exponents, in contrast to the existing theories which yield constant exponents. Moreover, the model reconciles the scaling at finite Reynolds number with the theoretical limit, where the enstrophy and dissipation rate scale identically at infinite Reynolds number. It suggests that the large-scale shear layers are vital for understanding the scaling of the extrema. Furthermore, to reach the theoretical limit, the scaling exponents must remain Reynolds number dependent beyond the present Reλ range.

We investigate the role of pressure, via its Hessian tensor 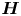${\boldsymbol {H}}$, on amplification of vorticity and strain-rate and contrast it with other inviscid nonlinear mechanisms. Results are obtained from direct numerical simulations of isotropic turbulence with Taylor-scale Reynolds number in the range 140–1300. Decomposing 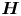${\boldsymbol {H}}$ into local isotropic (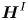${\boldsymbol {H}}^{I}$) and non-local deviatoric (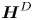${\boldsymbol {H}}^{D}$) components reveals that 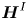${\boldsymbol {H}}^{I}$ depletes vortex stretching, whereas 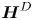${\boldsymbol {H}}^{D}$ enables it, with the former slightly stronger. The resulting inhibition is significantly weaker than the nonlinear mechanism which always enables vortex stretching. However, in regions of intense vorticity, identified using conditional statistics, contribution from 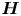${\boldsymbol {H}}$ prevails over nonlinearity, leading to overall depletion of vortex stretching. We also observe near-perfect alignment between vorticity and the eigenvector of 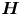${\boldsymbol {H}}$ corresponding to the smallest eigenvalue, which conforms with well-known vortex-tubes. We discuss the connection between this depletion, essentially due to (local) 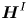${\boldsymbol {H}}^{I}$, and recently identified self-attenuation mechanism (Buaria et al., Nat. Commun., vol. 11, 2020, p. 5852), whereby intense vorticity is locally attenuated through inviscid effects. In contrast, the influence of 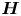${\boldsymbol {H}}$ on strain-amplification is weak. It opposes strain self-amplification, together with vortex stretching, but its effect is much weaker than vortex stretching. Correspondingly, the eigenvectors of strain and 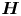${\boldsymbol {H}}$ do not exhibit any strong alignments. For all results, the dependence on Reynolds number is very weak. In addition to the fundamental insights, our work provides useful data and validation benchmarks for future modelling endeavours, for instance in Lagrangian modelling of velocity gradient dynamics, where conditional 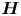${\boldsymbol {H}}$ is explicitly modelled.

We investigate the statistics of turbulence in emulsions of two immiscible fluids of the same density. We compute velocity increments between points conditioned to be located in the same phase or in different phases, and examine their probability density functions (PDFs) and the associated structure functions (SFs). This enables us to demonstrate that the presence of the interface reduces the skewness of the PDF at small scales and therefore the magnitude of the energy flux towards the dissipative scales, which is quantified by the third-order SF. The analysis of the higher-order SFs shows that multiphase turbulence is more intermittent than single-phase turbulence. In particular, the local scaling exponents of the SFs display a saturation below the Kolmogorov–Hinze scale, which indicates the presence of large velocity gradients across the interface. Interestingly, the statistics of the velocity differences in the carrier phase recovers that of single-phase turbulence when the viscosity of the dispersed phase is high.

The whistling induced by a low-Mach turbulent flow through a deep axisymmetric cavity in a duct is investigated theoretically and experimentally. The experiments include acoustic measurements and stereoscopic particle image velocimetry (PIV). The paper focuses on the effect of a mean swirl on the dynamics of the azimuthal aeroacoustic modes. The mean swirl in the cavity has two origins: one component is imposed by a controlled tangential air injection upstream of the cavity, and the other component spontaneously arises under the action of the self-sustained azimuthal aeroacoustic mode, as explained in the companion paper, Part 1 (Faure-Beaulieu, Xiong, Pedergnana & Noiray, J. Fluid Mech., vol. 971, 2023, A21). Experiments show that the dynamics of the aeroacoustic wave is influenced by the imposed swirl. In particular, the spinning wave propagating against the swirl is promoted. To explain this, a linear perturbation analysis is performed around an incompressible mean swirling flow obtained from RANS simulations. It reveals that the dominant shear layer modes of azimuthal order 1 and −1 involved in the whistling phenomenon are helical modes winding respectively with and against the swirl, and spinning respectively in counterswirl and co-swirl directions. The counterswirl hydrodynamic mode is the least damped of the two, which is in agreement with the experimental observations. Finally, a low-order model based on the wave equation is derived. With only a few parameters, it fully reproduces the experimental observations for a wide range of imposed swirl intensity in the duct flow, and it allows us to disentangle the mechanisms responsible for this complex aeroacoustic instability.

We study fluctuations of all co-existing energy exchange/transfer/transport processes in stationary periodic turbulence including those that average to zero and are not present in average cascade theories. We use a Helmholtz decomposition of accelerations that leads to a decomposition of all terms in the Kármán–Howarth–Monin–Hill (KHMH) equation (scale-by-scale two-point energy balance) causing it to break into two energy balances, one resulting from the integrated two-point vorticity equation and the other from the integrated two-point pressure equation. The various two-point acceleration terms in the Navier–Stokes difference (NSD) equation for the dynamics of two-point velocity differences have similar alignment tendencies with the two-point velocity difference, implying similar characteristics for the NSD and KHMH equations. We introduce the two-point sweeping concept and show how it articulates with the fluctuating interscale energy transfer as the solenoidal part of the interscale transfer rate does not fluctuate with turbulence dissipation at any scale above the Taylor length but with the sum of the time derivative and the solenoidal interspace transport rate terms. The pressure fluctuations play an important role in the interscale and interspace turbulence transfer/transport dynamics as the irrotational part of the interscale transfer rate is equal to the irrotational part of the interspace transfer rate and is balanced by two-point fluctuating pressure work. We also study the homogeneous/inhomogeneous decomposition of interscale transfer. The statistics of the latter are skewed towards forward cascade events whereas the statistics of the former are not. We also report statistics conditioned on intense forward/backward interscale transfer events.

This study aims to examine the spatial evolution of the geometrical features of the turbulent/turbulent interface (TTI) in a cylinder wake. The wake is exposed to various turbulent backgrounds in which the turbulence intensity and the integral length scale are varied independently, and comparisons to a turbulent/non-turbulent interface (TNTI) are drawn. The turbulent wake was marked with a high Schmidt number ($Sc$) scalar, and a planar laser induced fluorescence experiment was carried out to capture the interface between the wake and the ambient flow from $x/d = 5$ to 40, where $x$ is the streamwise coordinate from the centre of the cylinder, and $d$ is the cylinder's diameter. It is found that the TTI generally spreads faster towards the ambient flow than the TNTI. A transition region of the interfaces’ spreading is found at $x/d \approx 15$, after which the interfaces propagate at a slower rate than previously (upstream), and the mean interface positions of both the TNTI and TTI scale with the local wake half-width. The locations of both the TNTI and TTI have non-Gaussian probability density functions (PDFs) in the near wake because of the influence of the large-scale coherent motions present within the flow. Further downstream, after the large-scale coherent motions have dissipated, the TNTI position PDF does become Gaussian. For the first time, we explore the spatial variation of the ‘roughness’ of the TTI, quantified via the fractal dimension, from near field to far field. The length scale in the background flow has a profound effect on the TTI fractal dimension in the near wake, whilst the turbulence intensity becomes important only for the fractal dimension farther downstream.

The wall dependence of length scales used to describe large- and small-scale structures of turbulence is examined using highly resolved experiments in zero-pressure-gradient turbulent boundary layers and pipe flows spanning the range $2000< Re_\tau <37\ 700$. Of particular interest is the influence of external intermittency on the scaling of these length scales. It is found that when suitable scaling parameters are selected and external intermittency is accounted for, the dissipative motions follow inner scaling even into the outer-scaled regions of the flow, and that certain large-scale descriptions follow outer scaling even in the inner-scaled regions of the flow. The wall dependence is the same for both internal pipe and external boundary layer flows, and the different length scales can be related to recognizable features in the longitudinal wavenumber spectrum.

Direct numerical simulations (DNS) of temporally developing turbulent boundary layers are performed with a wide range of Reynolds numbers based on the momentum thickness $Re_{\theta } = 2000$–$13\,000$ for investigating the Reynolds number dependence of the turbulent/non-turbulent interface (TNTI) layer. The grid spacing in the DNS is determined carefully such that small-scale turbulent motions near the TNTI are well resolved. The outer edge of the TNTI layer, called the irrotational boundary, is detected with vorticity magnitude. The mean thicknesses of the TNTI layer, $\delta _{TNTI}$, turbulent sublayer, $\delta _{TSL}$, and viscous superlayer, $\delta _{VSL}$, are found to be approximately $15\eta _{TI}$, $10\eta _{TI}$ and $5\eta _{TI}$, respectively, where $\eta _{TI}$ is the Kolmogorov scale taken in the turbulent region near the TNTI layer. The mean curvature of the irrotational boundary is also characterized by $\eta _{TI}$. The shear parameter and the shear-to-vorticity ratio show that the mean shear effects near the TNTI layer are not significant for both large and small scales. The anisotropy tensors of Reynolds stress and vorticity suggest that the turbulence under the TNTI layer tends to be isotropic at high $Re_{\theta }$, for which $\eta _{TI}/\delta \sim Re_{\theta }^{-3/4}$ is valid with the boundary layer thickness $\delta$. The surface area of the irrotational boundary is consistent with the fractal analysis of the interface, where the fractal dimension $D_f$ is found to be $2.14$–$2.20$. The present results suggest that the mean entrainment rate per unit horizontal area normalized by the friction velocity varies slowly as $Re_{\theta }^{(3/4)(D_f-2)}$ for $Re_{\theta } \geq 4000$.

Dust storms are typical dispersed two-phase atmospheric turbulence involving electrified charged dust particles. Previous observations have demonstrated that clean-air atmospheric turbulence is strongly intermittent. However, the intermittency of the wind velocity, concentration of dust particles with a diameter smaller than $10\ \mathrm {\mu }{\rm m}$ (PM10) and electric fields, known as multifield intermittency, has not been reported or characterized yet. Here, we quantify the small-scale multifield intermittency of dust storms using datasets obtained from the Qingtu Lake Observation Array and a wavelet-based data analysis technique. The results indicate that the probability density functions of the multifield increments are scale dependent, and the scaling exponents of the multifield structure functions exhibit anomalous scaling, suggesting that the multiple fields in dust storms are also highly intermittent. Specifically, the wind velocity during dust storms appears to be more intermittent as compared with clean-air conditions. Among the multiple fields, the small-scale intermittency is strongest for PM10 dust concentration, moderate for electric fields and weakest for wind velocity. Furthermore, the anomalous scaling of multiple fields is well described by the hierarchical structure theory of turbulence. It is theoretically predicted that the wind velocity displays a one-dimensional filamentary structure, while the PM10 dust concentration and electric fields display two-dimensional sheet-like structures. Finally, after removing the coherent components of the observed time series by the proposed wavelet conditioning statistics, Kolmogorov linear scaling is recovered for the multiple fields, suggesting that small-scale multifield intermittency is caused by the presence of small-scale coherent structures.

Through direct numerical simulations we investigate the effects of spatiotemporal intermittency as a result of stable stratification in surface heated stratified open channel flow. By adapting the density inversion criterion method of Portwood et al. [J. Fluid Mech., vol. 807, 2016, R2] for our flow, we demonstrate that the flow may be robustly separated into regions of active turbulence for which $Re_B \gtrsim {O}(10)$ and surrounding quiescent fluid, where $Re_B$ is the buoyancy Reynolds number. The intermittency in the flow spontaneously manifests as a deformed horizontal interface between the upper quiescent and lower turbulent flow, characterised by vigorous mixing from ‘overturning’ shear instabilities. The resulting vertical intermittency profile is accurately predicted by a local Monin–Obukhov length normalised by viscous wall units $\varLambda ^+$ such that the flow displays intermittency within the parameter range of $2.5 \lesssim \varLambda ^+ \lesssim 260$. By considering conditional averages of the ‘turbulent’ and ‘quiescent’ flow separately, we find the ‘turbulent’ flow within this region to be described by constant critical gradient Richardson and turbulent Froude numbers of $Ri_{g,c} \approx 0.2$ and $Fr_c \approx 0.3$. We find that the turbulent flow continues to display a $\varGamma \sim Fr^{-1}$ relationship when $Fr < Fr_c$, whereas the quiescent flow shows no correlation between $\varGamma$ and $Fr$, where $\varGamma$ is the flux coefficient. Hence, we demonstrate directly that for our flow, the emergence of an asymptotic ‘saturated’ $\varGamma$ regime in the limit of a low ‘global’ $Fr$ occurs due to intermittency and increasing contributions to measurements of $\varGamma$ from the quiescent flow.

The Hall–Vinen–Bekharevich–Khalatnikov (HVBK) model is widely used to numerically study quantum turbulence in superfluid helium. Based on the two-fluid model of Tisza and Landau, the HVBK model describes the normal (viscous) and superfluid (inviscid) components of the flow using two Navier–Stokes type of equations, coupled through a mutual friction force term. We derive transport equations for the third-order moments for each component of velocity involving the fourth-order moments, which are classical probes for internal intermittency at any scale, and revealing the probability of rare and strong fluctuations. Budget equations are assessed through direct numerical simulations of the HVBK flow. We simulate a forced homogeneous isotropic turbulent flow with Reynolds number of the normal fluid (based on Taylor's microscale) close to 100. Values from 0.1 to 10 are considered for the ratio between the normal and superfluid densities. For these flows, an inertial range is not discernible and the restricted scaling range approach is used to take into account the finite Reynolds number (FRN) effect. We analyse the importance of each term in budget equations and emphasize their role in energy exchange between normal and superfluid components. Some interesting features are observed: (i) transport and pressure-related terms are dominant, similarly to single-fluid turbulence; and (ii) the mathematical signature of the FRN effect is weak despite the low value of the Reynolds number. The flatness of the velocity derivatives is finally studied through the transport equations and their limit for very small scales, and it is shown to gradually increase for lower and lower temperatures, for both normal fluid and superfluid. This similarity highlights the strong locking of the two fluids. The flatness factors are also found in reasonable agreement with classical turbulence.

Premixed turbulent flames, encountered in power generation and propulsion engines, are an archetype of a randomly advected, self-propagating surface. While such a flame is known to exhibit large-scale intermittent flapping, the possible intermittency of its small-scale fluctuations has been largely disregarded. Here, we experimentally reveal the inner intermittency of a premixed turbulent V-flame, while clearly distinguishing this small-scale feature from large-scale outer intermittency. From temporal measurements of the fluctuations of the flame, we find a frequency spectrum that has a power-law subrange with an exponent close to $-2$, which is shown to follow from Kolmogorov phenomenology. Crucially, however, the moments of the temporal increment of the flame position are found to scale anomalously, with exponents that saturate at higher orders. This signature of small-scale inner intermittency is shown to originate from high-curvature, cusp-like structures on the flame surface, which have significance for modelling the heat release rate and other key properties of premixed turbulent flames.