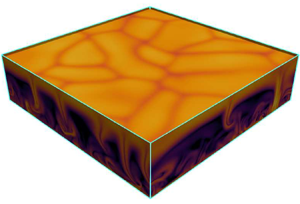
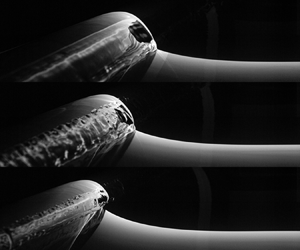
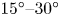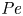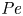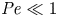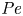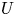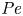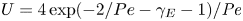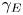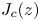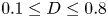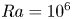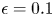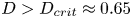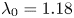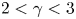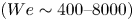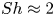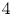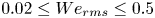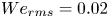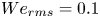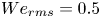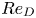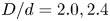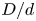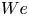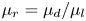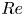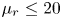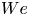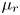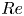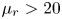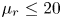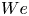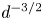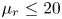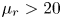doi:10.1017/jfm.2023.730 Zhong et al. From sheared annular centrifugal Rayleigh-Bénard convection to radially heated Taylor-Couette flow: exploring the impact of buoyancy and shear on heat transfer and flow structure
JFM Rapids
Pressure plateau of separation induced by shock impingement in a Mach 5 flow
-
- Published online by Cambridge University Press:
- 26 September 2023, R1
-
- Article
- Export citation
The influence of directional spreading on rogue waves triggered by abrupt depth transitions
-
- Published online by Cambridge University Press:
- 29 September 2023, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spontaneous autophoretic motion of isotropic disks
-
- Published online by Cambridge University Press:
- 04 October 2023, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compressible turbulent convection in highly stratified adiabatic background
-
- Published online by Cambridge University Press:
- 03 October 2023, R4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effects of surfactants on plunging breakers
-
- Published online by Cambridge University Press:
- 03 October 2023, R5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of parasitic gravity-capillary standing waves in the small surface tension limit
-
- Published online by Cambridge University Press:
- 04 October 2023, R6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact solutions for the initial stage of dam-break flow on a plane hillside or beach
-
- Published online by Cambridge University Press:
- 11 October 2023, R7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
Ineffective diffusivity
-
- Published online by Cambridge University Press:
- 02 October 2023, F1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
The effect of Navier slip on the rheology of a dilute two-dimensional suspension of plate-like particles
-
- Published online by Cambridge University Press:
- 26 September 2023, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixing enhancement of a compressible jet over a convex wall
-
- Published online by Cambridge University Press:
- 26 September 2023, A2
-
- Article
- Export citation
Scaling of boundary-layer disturbances exposed to free-stream turbulence
-
- Published online by Cambridge University Press:
- 26 September 2023, A3
-
- Article
- Export citation
Post-stall flow control on aerofoils by leading-edge flags
-
- Published online by Cambridge University Press:
- 26 September 2023, A4
-
- Article
- Export citation
A unified explanation of energy growth sources for unstable modes in flat-plate boundary layers
-
- Published online by Cambridge University Press:
- 26 September 2023, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
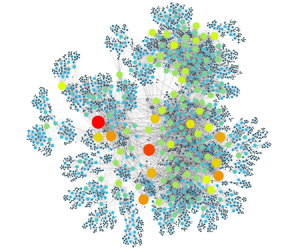
Multifractality and scale-free network topology in a noise-perturbed laminar jet
-
- Published online by Cambridge University Press:
- 26 September 2023, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shock-induced atomisation of a liquid metal droplet
-
- Published online by Cambridge University Press:
- 26 September 2023, A7
-
- Article
- Export citation
Interactions enhance dispersion in fluctuating channels via emergent flows
-
- Published online by Cambridge University Press:
- 27 September 2023, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the interaction of Taylor length-scale size droplets and homogeneous shear turbulence
-
- Published online by Cambridge University Press:
- 28 September 2023, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How vortex dynamics affects the structural load in step cylinder flow
-
- Published online by Cambridge University Press:
- 27 September 2023, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Role of viscosity in turbulent drop break-up
-
- Published online by Cambridge University Press:
- 27 September 2023, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the relationship between manipulated inter-scale phase and energy-efficient turbulent drag reduction
-
- Published online by Cambridge University Press:
- 26 September 2023, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation