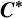 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
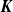 $\boldsymbol{K}$-theory, and traces
$\boldsymbol{K}$-theory, and traces
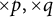 $\times p,\times q$ conjecture
$\times p,\times q$ conjecture
 $^*$-algebras
$^*$-algebras
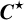 ${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS