Thermoacoustic instability – self-sustained pressure oscillations triggered by temperature gradients – has become an increasingly studied topic in the context of energy conversion. Generally, the process relies on conductive heat transfer between a solid and the fluid in which the generated pressure oscillations are sustained. In the present study, the thermoacoustic theory is extended to include mass transfer; specifically, the working fluid is modified so as to incorporate a ‘reactive’ gas, able to exchange phase with a solid/liquid boundary through a sorption process (or through evaporation/condensation), such that most heat is transferred in the form of latent heat rather than through conduction. A set of differential equations is derived, accounting for phase-exchange heat and mass transfer, and de-coupled via a small-amplitude asymptotic expansion. These equations are solved and subsequently manipulated into the form of a wave equation, representing the small perturbation on the pressure field, and used to derive expressions for the time-averaged, second-order heat and mass fluxes. A stability analysis is performed on the wave equation, from which the marginal stability curve is calculated in terms of the temperature difference, 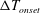 $\unicode[STIX]{x0394}T_{onset}$, required for initiation of self-sustained oscillations. Calculated stability curves are compared with published experimental results, showing good agreement. Effects of gas mixture composition are studied, indicating that a lower heat capacity of the inert component, combined with a low boiling temperature and high latent heat of the reactive component substantially lower
$\unicode[STIX]{x0394}T_{onset}$, required for initiation of self-sustained oscillations. Calculated stability curves are compared with published experimental results, showing good agreement. Effects of gas mixture composition are studied, indicating that a lower heat capacity of the inert component, combined with a low boiling temperature and high latent heat of the reactive component substantially lower 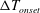 $\unicode[STIX]{x0394}T_{onset}$. Furthermore, an increase in the average mole fraction of the reactive gas,
$\unicode[STIX]{x0394}T_{onset}$. Furthermore, an increase in the average mole fraction of the reactive gas, 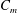 $C_{m}$ strongly affects onset conditions, leading to
$C_{m}$ strongly affects onset conditions, leading to 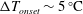 $\unicode[STIX]{x0394}T_{onset}\sim 5\,^{\circ }\text{C}$ at the highest value of
$\unicode[STIX]{x0394}T_{onset}\sim 5\,^{\circ }\text{C}$ at the highest value of 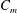 $C_{m}$ achievable under atmospheric pressure. An analysis of the system limit cycle is performed for a wide range of parameters, indicating a systematic decrease in the temperature difference capable of sustaining the limit cycle, as well as a significant distortion of the acoustic wave form as the phase-exchange mechanism becomes dominant. These findings, combined, reveal the underlying mechanisms by which a phase-exchange engine may produce more acoustic power than its counterpart ‘classical’ thermoacoustic system, while its temperature difference is substantially lower.
$C_{m}$ achievable under atmospheric pressure. An analysis of the system limit cycle is performed for a wide range of parameters, indicating a systematic decrease in the temperature difference capable of sustaining the limit cycle, as well as a significant distortion of the acoustic wave form as the phase-exchange mechanism becomes dominant. These findings, combined, reveal the underlying mechanisms by which a phase-exchange engine may produce more acoustic power than its counterpart ‘classical’ thermoacoustic system, while its temperature difference is substantially lower.