In this paper the asymmetric shock reflection configurations in two-dimensional steady flows have been studied theoretically. For an overall Mach reflection, it is found that the horizontal distance between both triple points in the Mach stem is related to the angles of two slip streams. Based on the features of the converging stream tube, several assumptions are put forward to perform better the wave configurations near the slip streams. Therefore, we present an analytical model here to describe the asymmetric overall Mach reflection configurations which agrees well with the computational and experimental results.

In this paper, we apply aeration with oxygen microbubbles to tap water; the intent is to quantitatively evaluate whether nitrogen gas originally dissolved in the water under the atmosphere is purged by the aeration with oxygen microbubbles. Oxygen microbubbles are continuously injected into the circulation system of tap water open to the atmosphere. While the concentration of dissolved oxygen (DO) can be detected by a commercial DO meter, that of dissolved nitrogen (DN) is unavailable. To detect the DN level, we observe the growth of millimetre-sized gas bubbles nucleated at glass surfaces in contact with the aerated water and compare it with the multi-species theory of Epstein and Plesset where the (unknown) DN concentration is treated as a fitting parameter. In the theory, we solve binary diffusion of each gas species (oxygen or nitrogen) in the water independently, under the assumption that the dissolved gases are sufficiently dilute. Comparisons between the experiment and the theory suggest that the DN in the water is effectively purged by the oxygen aeration. The supplemental experiment of aeration with nitrogen microbubbles is also documented to show that the DO can be effectively purged as well.

Acoustic fields in a liquid medium can trap and suspend small particles at their pressure nodes. Recent measurements demonstrate that nanorods immersed in these fields generate autonomous propulsion, with their direction and speed controlled by both the particle’s shape and density distribution. Specifically, slender nanorods with an asymmetric density distribution about their geometric centre are observed to move steadily with their low density end leading the motion; particle geometry exerts an equally significant and potentially opposing effect. In this article, we investigate the physical mechanisms underlying this combined density/shape induced phenomenon by developing a simple yet rigorous mathematical framework for axisymmetric particles. This only requires solution of the (linear) unsteady Stokes equations, which can be performed numerically or analytically. The theory holds for all particle shapes, particle aspect ratios (length/width) and acoustic frequencies. It is applied to slender dumbbell-shaped particles and asymmetric nanorods – these provide model systems to investigate the competing effects governing propulsion. This shows that geometric and density asymmetries in the particle generate axial jets that can produce motion in either direction, depending on the relative strengths of these asymmetries and the acoustic Reynolds number (dimensionless frequency). Strikingly, the propulsion direction is found to reverse with increasing frequency, an effect that is yet to be reported experimentally. The general theory and mechanism described here enable the a priori design and fabrication of nano-motors in fluid for transport of small-scale payloads and robotic applications.

We present a numerical study on particle migration in a planar extrudate flow of suspensions of non-Brownian hard spheres. The suspension is described as a Newtonian liquid with a concentration-dependent viscosity, and shear-induced particle migration is modelled according to the diffusive flux model. The fully coupled set of nonlinear differential equations governing the flow is solved with a stabilized finite element method together with the elliptic mesh generation method to compute the position of the free surface. We show that shear-induced particle migration inside the channel leads to a highly non-uniform particle concentration distribution under the free surface. It is found that particle migration dramatically changes the shape of the free surface when the suspension is compared to a Newtonian liquid with the same bulk properties. Remarkably, we observed extrudate expansion in the Newtonian and dilute suspension flows; in turn, at high concentrations, a die contraction appears. The model does not account for normal stress differences, and this result is a direct consequence of variations in the flow stress field caused by shear-induced particle migration.

The zonally symmetric inertial instability of oceanic near-equatorial flows is studied through high-resolution numerical simulations. In homogeneous upper layers, the instability of surface-confined westward currents implies potentially fast downward mixing of momentum with a predictable final equilibrium. With increasing Reynolds number, latitudinal scales along the surface associated with the instability become ever smaller and initially the motions are ever more concentrated underneath the surface. The results suggest that even if the upper layer is stratified, it may still be necessary to include the full Coriolis force in the dynamics rather than use the traditional $\unicode[STIX]{x1D6FD}$-plane approximation.

The role of passive body dynamics on the kinematics of swimming micro-organisms in complex fluids is investigated. Asymptotic analysis of small-amplitude motions of a finite-length undulatory swimmer in a Stokes–Oldroyd-B fluid is used to predict shape changes that result as body elasticity and fluid elasticity are varied. Results from the analysis are compared with numerical simulations and the numerically simulated shape changes agree with the analysis at both small and large amplitudes, even for strongly elastic flows. We compute a stroke-induced swimming speed that accounts for the shape changes, but not additional effects of fluid elasticity. Elasticity-induced shape changes lead to larger-amplitude strokes for sufficiently soft swimmers in a viscoelastic fluid, and these stroke boosts can lead to swimming speed-ups. However, for the strokes we examine, we find that additional effects of fluid elasticity generically result in a slow-down. Our high amplitude strokes in strongly elastic flows lead to a qualitatively different regime in which highly concentrated elastic stresses accumulate near swimmer bodies and dramatic slow-downs are seen.

The Nyquist–Shannon criterion indicates the sample rate necessary to identify information with particular frequency content from a dynamical system. However, in experimental applications such as the interrogation of a flow field using particle image velocimetry (PIV), it may be impracticable or expensive to obtain data at the desired temporal resolution. To address this problem, we propose a new approach to identify temporal information from undersampled data, using ideas from modal decomposition algorithms such as dynamic mode decomposition (DMD) and optimal mode decomposition (OMD). The novel method takes a vector-valued signal, such as an ensemble of PIV snapshots, sampled at random time instances (but at sub-Nyquist rate) and projects onto a low-order subspace. Subsequently, dynamical characteristics, such as frequencies and growth rates, are approximated by iteratively approximating the flow evolution by a low-order model and solving a certain convex optimisation problem. The methodology is demonstrated on three dynamical systems, a synthetic sinusoid, the cylinder wake at Reynolds number $Re=60$ and turbulent flow past the axisymmetric bullet-shaped body. In all cases the algorithm correctly identifies the characteristic frequencies and oscillatory structures present in the flow.

The vortical structures and turbulence statistics in the near wake of rectangular, trapezoidal, triangular and ellipsoidal tabs were experimentally studied in a refractive-index-matching channel. The tabs share the same bulk dimensions, including a 17 mm height, a 28 mm base width and a $24.5^{\circ }$ inclination angle. Measurements were performed at two Reynolds numbers based on the tab height, $Re_{h}\simeq 2000$ (laminar incoming flow) and 13 000 (turbulent incoming flow). Three-dimensional, three-component particle image velocimetry (PIV) was used to study the mean flow distribution and dominant large-scale vortices, while complementary high-spatial-resolution planar PIV measurements were used to quantify high-order statistics. Instantaneous three-dimensional fields revealed the coexistence of a coherent counter-rotating vortex pair (CVP) and hairpin structures. The CVP and hairpin vortices (the primary structures) exhibit distinctive characteristics and strength across $Re_{h}$ and tab geometries. The CVP is coherently present in the mean flow field and grows in strength over a significantly longer distance at the low $Re_{h}$ due to the lower turbulence levels and the delayed shedding of the hairpin vortices. These features at the low $Re_{h}$ are associated with the presence of Kelvin–Helmholtz instability that develops over three tab heights downstream of the trailing edge. Moreover, a secondary CVP with an opposite sense of rotation resides below the primary one for the four tabs at the low $Re_{h}$. The interaction between the hairpin structures and the primary CVP is experimentally measured in three dimensions and shows complex coexistence. Although the CVP undergoes deformation and splitting at times, it maintains its presence and leads to significant mean spanwise and wall-normal flows.

We study the instability mechanisms leading to slug flow formation in an inclined pipe subject to gravity forces. We use a phase-field approach, where the Cahn–Hillard model is used to model the interface. At the inlet, a stratified flow is imposed with a specified velocity profile. We validate our numerical results by comparing against previous theoretical models and by predicting the various flow regimes for horizontal and inclined pipes, including stratified flow, slug flow, dispersed bubble flow and annular flow. Subsequently, we focus on slug formation in an inclined pipe and connect its appearance with specific vortical dynamics. A two-dimensional channel geometry is first considered. When the heavy fluid is injected as the top layer, inverted vortex shedding emerges, which periodically impacts on the bottom wall, as it develops further downstream. The accumulation of heavy fluid in the bottom wall causes a back flow that induces rolling waves and interacts with the upstream jet. When the heavy fluid is placed as the bottom layer, the heavy fluid accumulates and initially forms a massive slug at the bottom region, close to the inlet. Subsequently, the heavy fluid slug starts to break into smaller pieces, some of which translate along the pipe. During the accumulation phase, a back flow forms also generating rolling waves. Occasionally, a rolling wave can reach the top of the pipe and form a new slug. To describe the generation of vorticity from the two-phase interface and pipe walls in the slug formation, we study the circulation dynamics and connect it with the resulting two-phase flow patterns. Finally, we conduct three-dimensional (3-D) simulations in a circular pipe and compare the differences between the 3-D flow patterns and its circulation dynamics against the 2-D simulation results.

Kelvin’s minimum energy theorem predicts that the irrotational motion of a homogeneously incompressible fluid in a simply connected region will carry less kinetic energy than any other profile that shares the same normal velocity conditions on the domain’s boundary. In this work, Kelvin’s analysis is extended to regions with boundaries on which the normal velocity requirements are relaxed. Given the ubiquity of practical configurations in which such boundaries exist, the question of whether Kelvin’s theorem continues to hold is one of significant interest. In reconstructing Kelvin’s proof, we find it useful to define a net rotational velocity as the difference between the generally rotational flow and the corresponding potential motion. In Kelvin’s classic theorem, the normal component of the net rotational velocity at all domain boundaries is zero. In contrast, the present analysis derives a sufficient condition for ensuring the validity of Kelvin’s theorem in a domain where the normal component of net rotational velocity at some or all of the boundaries is not zero. The corresponding criterion requires the evaluation of a simple surface integral over the boundary.

The Miles–Howard theorem states that a necessary condition for normal-mode instability in parallel, inviscid, steady stratified shear flows is that the minimum gradient Richardson number, $Ri_{g,min}$, is less than $1/4$ somewhere in the flow. However, the non-normality of the Navier–Stokes and buoyancy equations may allow for substantial perturbation energy growth at finite times. We calculate numerically the linear optimal perturbations which maximize the perturbation energy gain for a stably stratified shear layer consisting of a hyperbolic tangent velocity distribution with characteristic velocity $U_{0}^{\ast }$ and a uniform stratification with constant buoyancy frequency $N_{0}^{\ast }$. We vary the bulk Richardson number $Ri_{b}=N_{0}^{\ast 2}h^{\ast 2}/U_{0}^{\ast 2}$ (corresponding to $Ri_{g,min}$) between 0.20 and 0.50 and the Reynolds numbers $\mathit{Re}=U_{0}^{\ast }h^{\ast }/\unicode[STIX]{x1D708}^{\ast }$ between 1000 and 8000, with the Prandtl number held fixed at $\mathit{Pr}=1$. We find the transient growth of non-normal perturbations may be sufficient to trigger strongly nonlinear effects and breakdown into small-scale structures, thereby leading to enhanced dissipation and non-trivial modification of the background flow even in flows where $Ri_{g,min}>1/4$. We show that the effects of nonlinearity are more significant for flows with higher $\mathit{Re}$, lower $Ri_{b}$ and higher initial perturbation amplitude $E_{0}$. Enhanced kinetic energy dissipation is observed for higher-$Re$ and lower-$Ri_{b}$ flows, and the mixing efficiency, quantified here by $\unicode[STIX]{x1D700}_{p}/(\unicode[STIX]{x1D700}_{p}+\unicode[STIX]{x1D700}_{k})$ where $\unicode[STIX]{x1D700}_{p}$ is the dissipation rate of density variance and $\unicode[STIX]{x1D700}_{k}$ is the dissipation rate of kinetic energy, is found to be approximately 0.35 for the most strongly nonlinear cases.

The wake of an elliptical cylinder at low incident angles is investigated for different aspect ratio ($\unicode[STIX]{x1D6E4}=\text{major:minor axis ratio}$) cylinders using stability analysis and direct simulations. In particular, two- and three-dimensional transitions are mapped for cylinders of aspect ratios between 1 and 4 using Floquet stability analysis. The transition scenario for near-unity aspect ratio cylinders resembles that for a circular cylinder wake as Reynolds number is increased to $Re\lesssim 400$; first, with the transition from steady two-dimensional flow to unsteady two-dimensional flow, followed by the onset of three-dimensional flow via a long-wavelength instability (mode A), then, a short-wavelength instability (mode B) and, finally, an intermediary wavelength instability which is quasi-periodic in nature (mode QP). The effect of the incident angle on this transition scenario for the low-aspect-ratio cylinders is minimal. As the aspect ratio is increased towards 2, two synchronous modes, modes $\widehat{\text{A}}$ and $\widehat{\text{B}}$, become unstable; these modes have spatio-temporal symmetries similar to their circular cylinder wake counterparts, modes A and mode B, respectively. While mode $\widehat{\text{A}}$ persists for all incident angles investigated here, mode $\widehat{\text{B}}$ is found only to be unstable for incident angles up to $10^{\circ }$. Surprisingly, for $1.8\lesssim \unicode[STIX]{x1D6E4}\lesssim 2.9$, the mode A instability observed at zero incident angle emerges as a quasi-periodic mode as the incident angle is increased even slightly. At higher incident angles, this quasi-periodic mode once again transforms to a real mode on increasing the Reynolds number. The parameter space maps for the various aspect ratios are presented in the Reynolds number–incident angle plane, and the three-dimensional modes are discussed in terms of similarities to and differences from existing modes. A key aim of the work is to map the different modes and various transition sequences as a simple body geometry is systematically changed and as the flow symmetry is systematically broken; thus, insight is provided on the overall path towards fully turbulent flow.

We study the incipient motion of single spheres in steady shear flow on regular substrates at low particle Reynolds numbers. The substrate consists of a monolayer of regularly arranged fixed beads, in which the spacing between beads is varied resulting in different angles of repose and exposures of the particle to the main flow. The flow-induced forces and the level of flow penetration into the substrate are determined numerically. Since experiments in this range had shown that the critical Shields number is independent of inertia but strongly dependent on the substrate geometry, the particle Reynolds number was fixed to 0.01 in the numerical study. Numerics indicates that rolling motion is always preferred to sliding and that the flow penetration is linearly dependent on the spacing between the substrate particles. Besides, we propose an analytical model for the incipient motion. The model is an extension of Goldman’s classical result for a single sphere near a plain surface taking into account the angle of repose, flow orientation with respect to substrate topography and shielding of the sphere to the linear shear flow. The effective level of flow penetration is the only external parameter. The model, applied to triangular and quadratic arrangements with different spacings, is able to predict the dependence of the critical Shields number on the geometry and on the orientation of the substrate. The model is in very good agreement with numerical results. For well-exposed particles, we observed that the minimum critical Shields number for a certain angle of repose does not depend sensitively on the considered arrangement. At large angles of repose, as expected in fully armoured beds, the model is consistent with experimental results for erodible beds at saturated conditions.

We present a study of the turbulence cascade on the centreline of an inhomogeneous and anisotropic near-field turbulent wake generated by a square prism at a Reynolds number of $Re=3900$ using the Kármán–Howarth–Monin–Hill equation. This is the fully generalised scale-by-scale energy balance which, unlike the Kármán–Howarth equation, does not require homogeneity or isotropy assumptions. Our data are obtained from a direct numerical simulation and therefore enable us to access all of the processes involved in this energy balance. A significant range of length scales exists where the orientation-averaged nonlinear interscale transfer rate is approximately constant and negative, indicating a forward turbulence cascade on average. This average cascade consists of coexisting forward and inverse cascade behaviours in different scale-space orientations. With increasing distance from the prism but within the near field of the wake, the orientation-averaged nonlinear interscale transfer rate tends to be approximately equal to minus the turbulence dissipation rate even though all of the inhomogeneity-related energy processes in the scale-by-scale energy balance are significant, if not equally important. We also find well-defined near $-5/3$ energy spectra in the streamwise direction, in particular at a centreline position where the inverse cascade behaviour occurs for streamwise oriented length scales.

The system composed of a circular cylinder, either fixed or elastically mounted, and immersed in a current linearly sheared in the cross-flow direction, is investigated via numerical simulations. The impact of the shear and associated symmetry breaking are explored over wide ranges of values of the shear parameter (non-dimensional inflow velocity gradient, 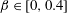$\unicode[STIX]{x1D6FD}\in [0,0.4]$) and reduced velocity (inverse of the non-dimensional natural frequency of the oscillator, 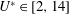$U^{\ast }\in [2,14]$), at Reynolds number 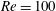$Re=100$; 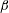$\unicode[STIX]{x1D6FD}$, 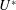$U^{\ast }$ and 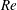$Re$ are based on the inflow velocity at the centre of the body and on its diameter. In the absence of large-amplitude vibrations and in the fixed body case, three successive regimes are identified. Two unsteady flow regimes develop for 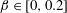$\unicode[STIX]{x1D6FD}\in [0,0.2]$ (regime L) and 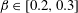$\unicode[STIX]{x1D6FD}\in [0.2,0.3]$ (regime H). They differ by the relative influence of the shear, which is found to be limited in regime L. In contrast, the shear leads to a major reconfiguration of the wake (e.g. asymmetric pattern, lower vortex shedding frequency, synchronized oscillation of the saddle point) and a substantial alteration of the fluid forcing in regime H. A steady flow regime (S), characterized by a triangular wake pattern, is uncovered for 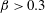$\unicode[STIX]{x1D6FD}>0.3$. Free vibrations of large amplitudes arise in a region of the parameter space that encompasses the entire range of 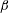$\unicode[STIX]{x1D6FD}$ and a range of 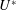$U^{\ast }$ that widens as 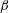$\unicode[STIX]{x1D6FD}$ increases; therefore vibrations appear beyond the limit of steady flow in the fixed body case (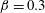$\unicode[STIX]{x1D6FD}=0.3$). Three distinct regimes of the flow–structure system are encountered in this region. In all regimes, body motion and flow unsteadiness are synchronized (lock-in condition). For 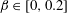$\unicode[STIX]{x1D6FD}\in [0,0.2]$, in regime VL, the system behaviour remains close to that observed in uniform current. The main impact of the shear concerns the amplification of the in-line response and the transition from figure-eight to ellipsoidal orbits. For 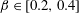$\unicode[STIX]{x1D6FD}\in [0.2,0.4]$, the system exhibits two well-defined regimes: VH1 and VH2 in the lower and higher ranges of 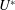$U^{\ast }$, respectively. Even if the wake patterns, close to the asymmetric pattern observed in regime H, are comparable in both regimes, the properties of the vibrations and fluid forces clearly depart. The responses differ by their spectral contents, i.e. sinusoidal versus multi-harmonic, and their amplitudes are much larger in regime VH1, where the in-line responses reach 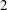$2$ diameters (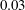$0.03$ diameters in uniform flow) and the cross-flow responses 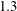$1.3$ diameters. Aperiodic, intermittent oscillations are found to occur in the transition region between regimes VH1 and VH2; it appears that wake–body synchronization persists in this case.

In order better to understand the processes that lead to the generation of magnetic fields of finite amplitude, we study dynamo action driven by turbulent Boussinesq convection in a rapidly rotating system. In the limit of infinite Prandtl number (the ratio of viscous to thermal diffusion) the inertia term drops out of the momentum equation, which becomes linear in the velocity. This simplification allows a decomposition of the velocity into a thermal part driven by buoyancy, and a magnetic part driven by the Lorentz force. While the former velocity defines the kinematic dynamo problem responsible for the exponential growth of the magnetic field, the latter encodes the magnetic back reaction that leads to the eventual nonlinear saturation of the dynamo. We argue that two different types of solution should exist: weak solutions in which the saturated velocity remains close to the kinematic one, and strong solutions in which magnetic forces drive the system into a new strongly magnetised state that is radically different from the kinematic one. Indeed, we find both types of solutions numerically. Interestingly, we also find that, in our inertialess system, both types of solutions exist on the same subcritical branch of solutions bifurcating from the non-magnetic convective state, in contrast with the more traditional situation for systems with finite inertia in which weak and strong solutions are thought to exist on different branches. We find that for weak solutions, the force balance is the same as in the non-magnetic case, with the horizontal size of the convection varying as the one-third power of the Ekman number (the ratio of viscous to Coriolis forces), which gives rise to very small cells at small Ekman numbers (i.e. high rotation rates). In the strong solutions, magnetic forces become important and the convection develops on much larger horizontal scales. However, we note that even in the strong cases the solutions never properly satisfy Taylor’s constraint, and that viscous stresses continue to play a role. Finally, we discuss the relevance of our findings to the study of planetary dynamos in rapidly rotating systems such as the Earth.

Cauchy invariants are now viewed as a powerful tool for investigating the Lagrangian structure of three-dimensional (3D) ideal flow (Frisch & Zheligovsky, Commun. Math. Phys., vol. 326, 2014, pp. 499–505; Podvigina et al., J. Comput. Phys., vol. 306, 2016, pp. 320–342). Looking at such invariants with the modern tools of differential geometry and of geodesic flow on the space SDiff of volume-preserving transformations (Arnold, Ann. Inst. Fourier, vol. 16, 1966, pp. 319–361), all manners of generalisations are here derived. The Cauchy invariants equation and the Cauchy formula, relating the vorticity and the Jacobian of the Lagrangian map, are shown to be two expressions of this Lie-advection invariance, which are duals of each other (specifically, Hodge dual). Actually, this is shown to be an instance of a general result which holds for flow both in flat (Euclidean) space and in a curved Riemannian space: any Lie-advection invariant $p$-form which is exact (i.e. is a differential of a $(p-1)$-form) has an associated Cauchy invariants equation and a Cauchy formula. This constitutes a new fundamental result in linear transport theory, providing a Lagrangian formulation of Lie advection for some classes of differential forms. The result has a broad applicability: examples include the magnetohydrodynamics (MHD) equations and various extensions thereof, discussed by Lingam et al. (Phys. Lett. A, vol. 380, 2016, pp. 2400–2406), and include also the equations of Tao (2016, arXiv:1606.08481 [math.AP]), Euler equations with modified Biot–Savart law, displaying finite-time blow-up. Our main result is also used for new derivations, and several new results, concerning local helicity-type invariants for fluids and MHD flow in flat or curved spaces of arbitrary dimension.

The point vortex is the simplest model of a two-dimensional vortex with non-zero circulation. The limitations introduced by its lack of core structure have been remedied by using desingularizations such as vortex patches and vortex sheets. We investigate steady states of the Sadovskii vortex in strain, a canonical model for a vortex in a general flow. The Sadovskii vortex is a uniform patch of vorticity surrounded by a vortex sheet. We recover previously known limiting cases of the vortex patch and hollow vortex, and examine the bifurcations away from these families. The result is a solution manifold spanned by two parameters. The addition of the vortex sheet to the vortex patch solutions immediately leads to splits in the solution manifold at certain bifurcation points. The more circular elliptical family remains attached to the family with a single pinch-off, and this family extends all the way to the simpler solution branch for the pure vortex sheet solutions. More elongated families below this one also split at bifurcation points, but these families do not exist in the vortex sheet limit.

Granular flows such as landslides, debris flows and avalanches are systems of particles with a large range of particle sizes that typically segregate while flowing. The physical mechanisms responsible for this process, however, are still poorly understood, and there is no predictive framework for ascertaining the segregation behaviour of a given system of particles. Here, we provide experimental evidence of individual large intruder particles being attracted to a fixed point in a dry two-dimensional flow of particles of otherwise uniform size. A continuum theory is proposed which captures this effect using only a single fitting parameter that describes the rate of segregation, given knowledge of the bulk flow field. Predictions of the continuum theory are compared with the experimental findings, both for the typical location and velocity field of a range of intruder sizes. For large intruder particle sizes, the continuum model successfully predicts that a fixed point attractor will form, where intruders are drawn to a single location.

The present paper investigates the influence of dense gases governed by complex equations of state on the dynamics of homogeneous isotropic turbulence. In particular, we investigate how differences due to the complex thermodynamic behaviour and transport properties affect the small-scale structures, viscous dissipation and enstrophy generation. To this end, we carry out direct numerical simulations of the compressible Navier–Stokes equations supplemented by advanced dense gas constitutive models. The dense gas considered in the study is a heavy fluorocarbon (PP11) that is shown to exhibit an inversion zone (i.e. a region where the fundamental derivative of gas dynamics $\unicode[STIX]{x1D6E4}$ is negative) in its vapour phase, for pressures and temperatures of the order of magnitude of the critical ones. Simulations are carried out at various initial turbulent Mach numbers and for two different initial thermodynamic states, one immediately outside and the other inside the inversion zone. After investigating the influence of dense gas effects on the time evolution of mean turbulence properties, we focus on the statistical properties of turbulent structures. For that purpose we carry out an analysis in the plane of the second and third invariant of the deviatoric strain-rate tensor. The analysis shows a weakening of compressive structures and an enhancement of expanding ones. Strong expansion regions are found to be mostly populated by non-focal convergence structures typical of strong compression regions, in contrast with the perfect gas that is dominated by eddy-like structures. Additionally, the contribution of non-focal expanding structures to the dilatational dissipation is comparable to that of compressed structures. This is due to the occurrence of steep expansion fronts and possibly of expansion shocklets which contribute to enstrophy generation in strong expansion regions and that counterbalance enstrophy destruction by means of the eddy-like structures.