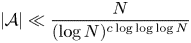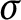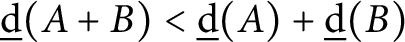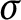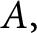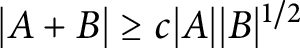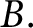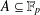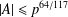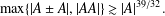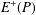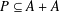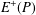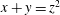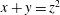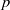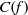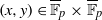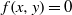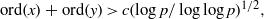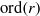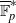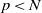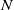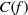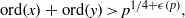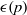Refine search
Actions for selected content:
13 results
A new upper bound for sets with no square differences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 30 September 2022, pp. 1777-1798
- Print publication:
- August 2022
-
- Article
- Export citation

Polynomial Methods and Incidence Theory
-
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022
Kneser’s theorem in
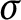 $\sigma $-finite abelian groups
$\sigma $-finite abelian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 936-942
- Print publication:
- December 2022
-
- Article
- Export citation
Sumsets of semiconvex sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 84-94
- Print publication:
- March 2022
-
- Article
- Export citation
EXPONENTIAL SUMS AND ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 506-508
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation

Introduction to Approximate Groups
-
- Published online:
- 31 October 2019
- Print publication:
- 14 November 2019
Higher-rank Bohr sets and multiplicative diophantine approximation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 24 September 2019, pp. 2214-2233
- Print publication:
- November 2019
-
- Article
- Export citation
A NEW SUM–PRODUCT ESTIMATE IN PRIME FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 268-280
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Monochromatic Solutions to
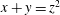 $x+y=z^{2}$
$x+y=z^{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 579-605
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
The additive group of the rationals does not have an automatic presentation
-
- Journal:
- The Journal of Symbolic Logic / Volume 76 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1341-1351
- Print publication:
- December 2011
-
- Article
- Export citation
Approximate groups. I The torsion-free nilpotent case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 02 June 2010, pp. 37-57
- Print publication:
- January 2011
-
- Article
- Export citation
EXPANSION OF ORBITS OF SOME DYNAMICAL SYSTEMS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 232-239
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation