We obtain new results about the number of trinomials 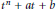 ${{t}^{n}}\,+\,at\,+\,b$ with integer coefficients in a box
${{t}^{n}}\,+\,at\,+\,b$ with integer coefficients in a box 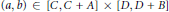 $(a,\,b)\,\in \,[C,\,C\,+\,A]\,\times \,[D,\,D\,+\,B]$ that are irreducible modulo a prime
$(a,\,b)\,\in \,[C,\,C\,+\,A]\,\times \,[D,\,D\,+\,B]$ that are irreducible modulo a prime 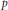 $p$. As a by-product we show that for any
$p$. As a by-product we show that for any 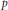 $p$ there are irreducible polynomials of height at most
$p$ there are irreducible polynomials of height at most 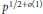 ${{p}^{1/2+o(1)}}$, improving on the previous estimate of
${{p}^{1/2+o(1)}}$, improving on the previous estimate of 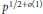 ${{p}^{2/3+o(1)}}$ obtained by the author in 1989.
${{p}^{2/3+o(1)}}$ obtained by the author in 1989.
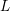 $L$-functions to prime power moduli
$L$-functions to prime power moduli