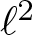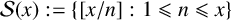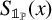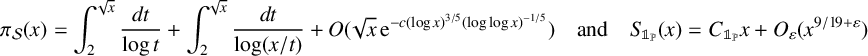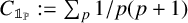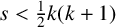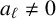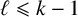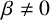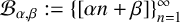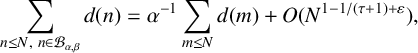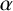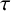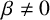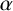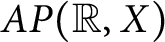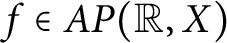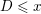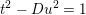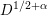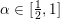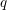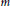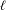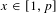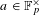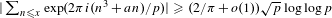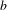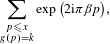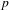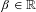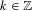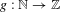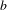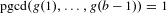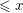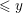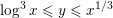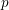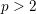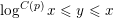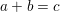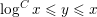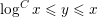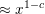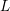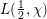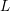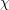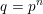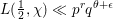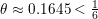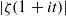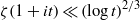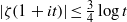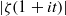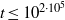43 results
BINARY AND TERNARY CONGRUENCES INVOLVING INTERVALS AND SETS MODULO A PRIME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1-11
-
- Article
- Export citation
Exponential sums over Möbius convolutions with applications to partitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-36
-
- Article
- Export citation
Full Poissonian local statistics of slowly growing sequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 148-180
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
- Export citation
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
- Export citation
ON THE PRIMES IN FLOOR FUNCTION SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 236-243
- Print publication:
- October 2023
-
- Article
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIVISOR FUNCTION OVER NONHOMOGENEOUS BEATTY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 280-287
- Print publication:
- October 2022
-
- Article
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Variations on Bombieri–Vinogradov
-
- Book:
- Bounded Gaps Between Primes
- Published online:
- 10 September 2021
- Print publication:
- 25 February 2021, pp 327-450
-
- Chapter
- Export citation
Explicit asymptotics for certain single and double exponential sums
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 607-632
- Print publication:
- April 2020
-
- Article
- Export citation
Counting fundamental solutions to the Pell equation with prescribed size
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2379-2402
- Print publication:
- November 2018
-
- Article
- Export citation
The Rudin–Shapiro Sequence and Similar Sequences Are Normal Along Squares
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1096-1129
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF THE MAXIMUM OF CUBIC EXPONENTIAL SUMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1259-1286
- Print publication:
- July 2020
-
- Article
- Export citation
BOUNDS FOR TRIPLE EXPONENTIAL SUMS WITH MIXED EXPONENTIAL AND LINEAR TERMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 64-69
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
On Euler's function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 April 2016, pp. 769-775
- Print publication:
- August 2016
-
- Article
- Export citation
Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 23 February 2016, pp. 1121-1158
- Print publication:
- June 2016
-
- Article
- Export citation
Sub-Weyl subconvexity for Dirichlet L-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
A NEW UPPER BOUND FOR \vert \zeta (1+ it)\vert
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 259-264
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation