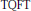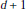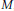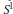20 results
On the Jones polynomial modulo primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 August 2023, pp. 730-734
- Print publication:
- September 2023
-
- Article
- Export citation
Torsion in thin regions of Khovanov homology
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 29 January 2021, pp. 630-654
- Print publication:
- June 2022
-
- Article
- Export citation
Chiral smoothings of knots
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 06 November 2020, pp. 1048-1061
-
- Article
- Export citation
A splicing formula for the LMO invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 1743-1770
- Print publication:
- December 2021
-
- Article
- Export citation
An intra-aortic guide wire: what “knot” to do
-
- Journal:
- Cardiology in the Young / Volume 30 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 09 December 2019, pp. 273-274
-
- Article
- Export citation
Burau Maps and Twisted Alexander Polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 27 February 2018, pp. 479-497
-
- Article
- Export citation
ON KILLERS OF CABLE KNOT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 171-176
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
55 - Gardens
- from Part VI - Visual Arts
-
-
- Book:
- The Cambridge Guide to the Worlds of Shakespeare
- Published online:
- 17 August 2019
- Print publication:
- 21 January 2016, pp 425-434
-
- Chapter
- Export citation
Part VI - Visual Arts
-
-
- Book:
- The Cambridge Guide to the Worlds of Shakespeare
- Published online:
- 17 August 2019
- Print publication:
- 21 January 2016, pp 375-482
-
- Chapter
- Export citation
COEXISTENCE OF COILED SURFACES AND SPANNING SURFACES FOR KNOTS AND LINKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 250-259
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
KNOT SINGULARITIES OF HARMONIC MORPHISMS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 44 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 20 January 2009, pp. 71-85
-
- Article
-
- You have access
- Export citation
Modified quantum dimensions and re-normalized link invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 196-212
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
On Non-Integral Dehn Surgeries Creating Non-Orientable Surfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 4 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 624-627
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation
Normal surfaces in non-compact 3-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-321
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
CONFORMALLY INVARIANT ENERGIES OF KNOTS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 4 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 08 March 2005, pp. 219-280
- Print publication:
- April 2005
-
- Article
- Export citation
The volume of hyperbolic alternating link complements
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 88 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 13 January 2004, pp. 204-224
- Print publication:
- January 2004
-
- Article
- Export citation
Topological Quantum Field Theory and Strong Shift Equivalence
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 2 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-197
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation
On the Homology of Finite Abelian Coverings of Links
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 3 / 01 September 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 309-315
- Print publication:
- 01 September 1997
-
- Article
-
- You have access
- Export citation
On the Minimal Crossing Number and the Braid Index of Links
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 1 / 01 February 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-131
- Print publication:
- 01 February 1993
-
- Article
-
- You have access
- Export citation
Ribbon knot families via stallings' twists
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 356-372
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation

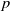
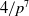
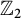
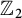
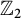
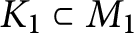
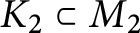
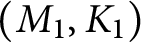
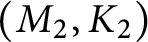
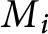
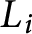
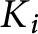
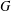
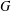
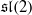 at a root of unity. These invariants contain Kashaev’s quantum dilogarithm invariants of knots.
at a root of unity. These invariants contain Kashaev’s quantum dilogarithm invariants of knots. , when normalized, will contain only a finite number of
, when normalized, will contain only a finite number of