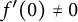ON THE ITERATIONS AND THE ARGUMENT DISTRIBUTION OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 145-170
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Improved Bloch and Landau constants for meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1269-1273
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Simple Proof and Strengthening of a Uniqueness Theorem for L-functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-122
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
ON THE ESCAPING SET OF MEROMORPHIC FUNCTIONS WITH DIRECT TRACTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 68-76
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
THE TUMURA–CLUNIE THEOREM IN SEVERAL COMPLEX VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 444-456
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF MEROMORPHIC FUNCTIONS WITH WEAKLY WEIGHTED SHARING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 26-43
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
NORMAL FAMILIES OF ZERO-FREE MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 16 November 2011, pp. 313-322
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Wiener-Hopf Factorization for a Family of Lévy Processes Related to Theta Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1023-1033
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
NORMALITY AND SHARED SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 01 June 2009, pp. 339-354
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
NEW CHARACTERIZATIONS OF THE MEROMORPHIC BESOV, Qp AND RELATED CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 49-58
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
THE SECOND DERIVATIVE OF A MEROMORPHIC FUNCTION
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 44 / Issue 3 / October 2001
- Published online by Cambridge University Press:
- 20 January 2009, pp. 455-478
-
- Article
-
- You have access
- Export citation
ZEROS OF DIFFERENTIAL POLYNOMIALS IN REAL MEROMORPHIC FUNCTIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 48 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 23 May 2005, pp. 279-293
-
- Article
-
- You have access
- Export citation
On the value distribution of f2f(k)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-26
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Further results on meromorphic functions that share two values with their derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-102
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Normality and exceptional functions of derivatives
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-414
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
ON A THEOREM OF A. A. GOL’DBERG
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 27 May 2004, pp. 125-129
-
- Article
-
- You have access
- Export citation
A note on normality and shared values
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-150
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
On normal families of meromorphic functions
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 155-164
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
On transcendental meromorphic functions which are geometrically finite
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-108
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Non-linear differential equations with transcendental meromorphic solutions
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 88-118
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation