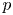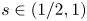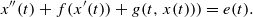14 results
Periodic solutions of p-Laplacian differential equations with jumping nonlinearity across half-eigenvalues
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 07 January 2022, pp. 307-326
- Print publication:
- February 2023
-
- Article
- Export citation
Periodic solutions for one-dimensional nonlinear nonlocal problem with drift including singular nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 December 2021, pp. 229-261
- Print publication:
- February 2023
-
- Article
- Export citation
On Periodic Solutions to Constrained Lagrangian System
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 242-255
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Periodic Solutions of an Indefinite Singular Equation Arising from the Kepler Problem on the Sphere
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-190
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
Nonlinear Dynamical Behaviour in a Predator-Prey Model with Harvesting
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 376-395
- Print publication:
- May 2017
-
- Article
- Export citation
Periodic Solutions of Almost Linear Volterra Integro-dynamic Equations on Periodic Time Scales
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 174-181
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
Numerical Approximation of Hopf Bifurcation for Tumor-Immune System Competition Model with Two Delays
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 5 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 146-162
- Print publication:
- April 2013
-
- Article
- Export citation
Complex Dynamics in Predator-prey Models with NonmonotonicFunctional Response and Harvesting
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 5 / 2013
- Published online by Cambridge University Press:
- 17 September 2013, pp. 95-118
- Print publication:
- 2013
-
- Article
- Export citation
Periodic Solutions in a Mathematical Model for the Treatment ofChronic Myelogenous Leukemia
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 7 / Issue 1 / 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 235-244
- Print publication:
- 2012
-
- Article
- Export citation
A NOTE ON PERIODIC SOLUTIONS OF A FORCED LIÉNARD-TYPE EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 3 / January 2010
- Published online by Cambridge University Press:
- 27 September 2010, pp. 350-368
-
- Article
-
- You have access
- Export citation
PERIODIC SOLUTIONS OF SINGULAR DIFFERENTIAL EQUATIONS WITH SIGN-CHANGING POTENTIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 14 September 2010, pp. 437-445
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
EXISTENCE AND STABILITY OF PERIODIC SOLUTIONS OF A RAYLEIGH TYPE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-390
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Extremal solutions and strong relaxation for nonlinear periodic evolution inclusions
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 3 / October 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 569-586
-
- Article
-
- You have access
- Export citation
Oscillation and Global Attractivity in a Periodic Delay Equation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 3 / 01 September 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 275-283
- Print publication:
- 01 September 1996
-
- Article
-
- You have access
- Export citation