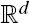We aim to link random fields and marked point processes, and, therefore, introduce a new class of stochastic processes which are defined on a random set in . Unlike for random fields, the mark covariance function of a random marked set is in general not positive definite. This implies that in many situations the use of simple geostatistical methods appears to be questionable. Surprisingly, for a special class of processes based on Gaussian random fields, we do have positive definiteness for the corresponding mark covariance function and mark correlation function.

We discuss the determination of the mean normal measure of a stationary random set Z ⊂ ℝd by taking measurements at the intersections of Z with k-dimensional planes. We show that mean normal measures of sections with vertical planes determine the mean normal measure of Z if k ≥ 3 or if k = 2 and an additional mild assumption holds. The mean normal measures of finitely many flat sections are not sufficient for this purpose. On the other hand, a discrete mean normal measure can be verified (i.e. an a priori guess can be confirmed or discarded) using mean normal measures of intersections with m suitably chosen planes when m ≥ ⌊d / k⌋ + 1. This even holds for almost all m-tuples of k-dimensional planes are viable for verification. A consistent estimator for the mean normal measure of Z, based on stereological measurements in vertical sections, is also presented.

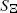The random surface measure of a stationary Boolean model with grains from the convex ring is considered. A sufficient condition and a necessary condition for the existence of the density of the second-order moment measure of are given and a representation of this density is derived. As applications, the surface pair correlation functions of a Boolean model with spheres and a Boolean model with randomly oriented right circular cylinders in ℝ3 are determined.

We study a random field obtained by counting the number of balls containing a given point when overlapping balls are thrown at random according to a Poisson random measure. We describe a microscopic process which exhibits multifractional behavior. We are particularly interested in the local asymptotic self-similarity (LASS) properties of the field, as well as in its X-ray transform. We obtain two different LASS properties when considering the asymptotics either in law or in the sense of second-order moments, and prove a relationship between the LASS behavior of the field and the LASS behavior of its X-ray transform. These results can be used to model and analyze porous media, images, or connection networks.

A spectral theory for stationary random closed sets is developed and provided with a sound mathematical basis. The definition and a proof of the existence of the Bartlett spectrum of a stationary random closed set as well as the proof of a Wiener-Khinchin theorem for the power spectrum are used to two ends. First, well-known second-order characteristics like the covariance can be estimated faster than usual via frequency space. Second, the Bartlett spectrum and the power spectrum can be used as second-order characteristics in frequency space. Examples show that in some cases information about the random closed set is easier to obtain from these characteristics in frequency space than from their real-world counterparts.

In the statistical analysis of random sets, it is useful to have simple statistics that can be used to describe the realizations of these sets. The cumulants and several other standardized moments such as the correlation and second cumulant can be used for this purpose, but their estimators can be excessively variable if the most straightforward estimation strategy is used. Through exploitation of similarities between this estimation problem and a similar one for a point process statistic, two modifications are proposed. Analytical results concerning the effects of these modifications are found through use of a specialized asymptotic regime. Simulation results establish that the modifications are highly effective at reducing estimator standard deviations for Boolean models. The results suggest that the reductions in variance result from a balanced use of information in the estimation of the first and second moments, through eliminating the use of observations that are not used in second moment estimation.

The germ-grain model is defined as the union of independent identically distributed compact random sets (grains) shifted by points (germs) of a point process. The paper introduces a family of stationary random measures in ℝd generated by germ-grain models and defined by the sum of contributions of non-overlapping parts of the individual grains. The main result of the paper is the central limit theorem for these random measures, which holds for rather general independently marked germ-grain models, including those with non-Poisson distribution of germs and non-convex grains. It is shown that this construction of random measures includes those random measures obtained by positively extended intrinsic volumes. In the Poisson case it is possible to prove a central limit theorem under weaker assumptions by using approximations by m-dependent random fields. Applications to statistics of the Boolean model are also discussed. They include a standard way to derive limit theorems for estimators of the model parameters.

We consider a stationary germ-grain model Ξ with convex and compact grains and the distance r(x) from x ε ℝd to Ξ. For almost all points x ε ℝd there exists a unique point p(x) in the boundary of Ξ such that r(x) is the length of the vector x-p(x), which is called the spherical contact vector at x. In this paper we relate the distribution of the spherical contact vector to the times it takes a typical boundary point of Ξ to hit another grain if all grains start growing at the same time and at the same speed. The notion of a typical point is made precise by using the generalized curvature measures of Ξ. The result generalizes a well known formula for the Boolean model. Specific examples are discussed in detail.

This paper considers estimators of parameters of the Boolean model which are obtained by means of the method of intensities. For an estimator of the intensity of the point process of germ points the asymptotic normality is proved and the corresponding variance is given. The theory is based on a study of second-order characteristics of the point process of lower-positive tangent points of the Boolean model. An estimator of the distribution of a typical grain is also discussed.

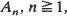Let , be i.i.d. random closed sets in 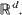. Limit theorems for their normalized convex hulls 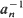conv (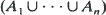) are proved. The limiting distributions correspond to 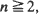C-stable random sets. The random closed set A is called C-stable if, for any , the sets 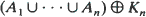anA and conv ( coincide in distribution for certain positive an, compact Kn, and independent copies A1, …, An of A. The distributions of C-stable sets are characterized via corresponding containment functionals.

An index lying between 0 and 1 is presented to describe the degree of liberation (or separation) of one component of a particulate material. It is shown how the index is related to the covariance function of the material, the distribution of shapes and sizes of the particles and to the interaction between fracture surfaces and the structure of the material. The variation of the index with the extent of crushing is investigated, together with the problem of stereological estimation. The index is evaluated for some particular probability models.

We shall discuss asymptotic properties of stereological estimators of volume (area) fraction for stationary random sets (in the sense of Matheron) under natural and general assumptions. Results obtained are strong consistency, asymptotic normality, and asymptotic unbiasedness and consistency of asymptotic variance estimators. The method is analogous to the non-parametric estimation of spectral density functions of stationary time series using window functions. Proofs are given for areal estimators, but they are also valid for lineal and point estimators with slight modifications. Finally we show that stationary Boolean models satisfy the relevant assumptions reasonably well.

Using the isomorphism between convex subsets of Euclidean space and continuous functions on the unit sphere we describe the probability measure of the convex hull of a random sample. When the sample is spherically symmetric the asymptotic behavior of this measure is determined. There are three distinct limit measures, each corresponding to one of the classical extreme-value distributions. Several properties of each limit are determined.