20 results
On the optimality of linear residual risk sharing
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA , First View
- Published online by Cambridge University Press:
- 10 January 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MONTE CARLO VARIANCE REDUCTION METHODS WITH APPLICATIONS IN STRUCTURAL RELIABILITY ANALYSIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 518-521
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
A multi-level procedure for enhancing accuracy of machine learning algorithms
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 14 July 2020, pp. 436-469
-
- Article
- Export citation
Asymptotic variance for random walk Metropolis chains in high dimensions: logarithmic growth via the Poisson equation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 994-1026
- Print publication:
- December 2019
-
- Article
- Export citation
Efficient simulation of Brown‒Resnick processes based on variance reduction of Gaussian processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1155-1175
- Print publication:
- December 2018
-
- Article
- Export citation
On spherical Monte Carlo simulations for multivariate normal probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 817-836
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
On the Acceleration of the Multi-Level Monte Carlo Method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 307-322
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Monte Carlo Simulation of Characteristic Secondary Fluorescence in Electron Probe Microanalysis of Homogeneous Samples Using the Splitting Technique
-
- Journal:
- / Volume 21 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 18 May 2015, pp. 753-758
- Print publication:
- June 2015
-
- Article
- Export citation
Simulation Analysis of System Life when Component Lives are Determined by a Marked Point Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 377-386
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Improving the Asmussen–Kroese-Type Simulation Estimators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1188-1193
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Efficient simulation of tail probabilities of sums of dependent random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 147-164
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Low-variance direct Monte Carlo simulationsusing importance weights
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 1069-1083
- Print publication:
- September 2010
-
- Article
- Export citation
Does Waste Recycling Really Improve the Multi-Proposal Metropolis–Hastings algorithm? an Analysis Based on Control Variates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 938-959
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Adaptive simulation using perfect control variates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 859-876
- Print publication:
- September 2004
-
- Article
- Export citation
Simulation of transient performance measures for stiff markov chains
-
- Journal:
- RAIRO - Operations Research / Volume 34 / Issue 4 / October 2000
- Published online by Cambridge University Press:
- 15 August 2002, pp. 385-396
- Print publication:
- October 2000
-
- Article
- Export citation
On the transient delays of M/G/1 queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 882-893
- Print publication:
- September 1999
-
- Article
- Export citation
Stochastic monotonicity and conditional Monte Carlo for likelihood ratios
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 103-115
- Print publication:
- March 1993
-
- Article
- Export citation
Processes with associated increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 313-333
- Print publication:
- June 1992
-
- Article
- Export citation
Monte Carlo simulation of the renewal function
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 2 / June 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-434
- Print publication:
- June 1981
-
- Article
- Export citation
Comparing stochastic systems using regenerative simulation with common random numbers
-
- Journal:
- Advances in Applied Probability / Volume 11 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 01 July 2016, pp. 804-819
- Print publication:
- December 1979
-
- Article
- Export citation

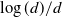
 A similar estimator converges at rate
A similar estimator converges at rate 