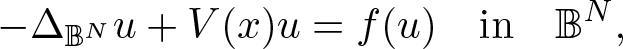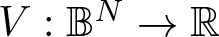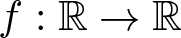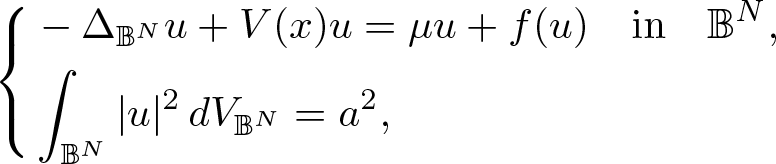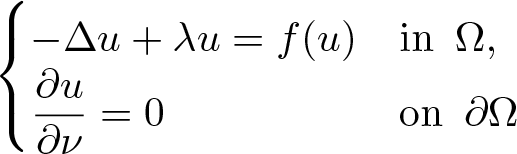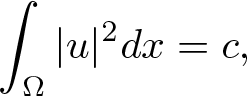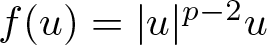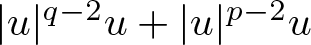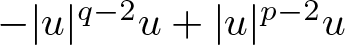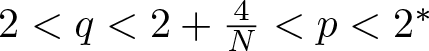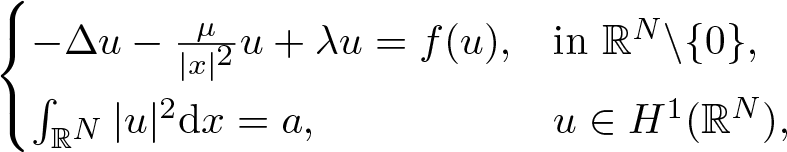Refine search
Actions for selected content:
190 results
Back-in-time analysis of vorticity in viscous separated flows over immersed bodies
-
- Journal:
- Journal of Fluid Mechanics / Volume 1024 / 10 December 2025
- Published online by Cambridge University Press:
- 09 December 2025, A46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Far field asymptotics of nematic flows around a small spherical particle
-
- Journal:
- Journal of Fluid Mechanics / Volume 1024 / 10 December 2025
- Published online by Cambridge University Press:
- 04 December 2025, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On nonlinear transitions, minimal seeds and exact solutions for the geodynamo
-
- Journal:
- Journal of Fluid Mechanics / Volume 1021 / 25 October 2025
- Published online by Cambridge University Press:
- 23 October 2025, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the existence of positive solutions to some classes of elliptic problems in Hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-41
-
- Article
- Export citation
Radial and non-radial solutions for a class of (p, q)-Laplace equations involving weights
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 July 2025, pp. 1-33
-
- Article
- Export citation
Modulation leading to frequency downshifting of water waves in the vicinity of the Benjamin–Feir transition
-
- Journal:
- Journal of Fluid Mechanics / Volume 1014 / 10 July 2025
- Published online by Cambridge University Press:
- 03 July 2025, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Local Inpainting Methods
-
- Book:
- The Art of Inpainting
- Published online:
- 22 May 2025
- Print publication:
- 22 May 2025, pp 13-51
-
- Chapter
- Export citation
3 - Non-Local Inpainting Methods
-
- Book:
- The Art of Inpainting
- Published online:
- 22 May 2025
- Print publication:
- 22 May 2025, pp 52-114
-
- Chapter
- Export citation
Learning rheological parameters of non-Newtonian fluids from velocimetry data
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 14 May 2025, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Most likely noise-induced tipping of the overturning circulation in a two-dimensional Boussinesq fluid model
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 21 April 2025, A53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variational data assimilation in wall turbulence: from outer observations to wall stress and pressure
-
- Journal:
- Journal of Fluid Mechanics / Volume 1008 / 10 April 2025
- Published online by Cambridge University Press:
- 03 April 2025, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solutions with prescribed mass for L2-supercritical NLS equations under Neumann boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple solutions for some classes of non-linear elliptic equations with variable exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-51
-
- Article
- Export citation
Internally heated convection with rotation: bounds on heat transport
-
- Journal:
- Journal of Fluid Mechanics / Volume 1001 / 25 December 2024
- Published online by Cambridge University Press:
- 19 December 2024, A55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding heat transport in supergravitational turbulent thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 1001 / 25 December 2024
- Published online by Cambridge University Press:
- 19 December 2024, A56
-
- Article
- Export citation
Normalized ground state solutions for critical growth Schrödinger equations with Hardy potential
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-30
-
- Article
- Export citation
On the inviscid instability of the 2-D Taylor–Green vortex
-
- Journal:
- Journal of Fluid Mechanics / Volume 999 / 25 November 2024
- Published online by Cambridge University Press:
- 20 November 2024, A64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the origin of counter-gradient transport in turbulent scalar flux: physics interpretation and adjoint data assimilation
-
- Journal:
- Journal of Fluid Mechanics / Volume 999 / 25 November 2024
- Published online by Cambridge University Press:
- 19 November 2024, A81
-
- Article
- Export citation
Internal heating profiles for which downward conduction is impossible
-
- Journal:
- Journal of Fluid Mechanics / Volume 993 / 25 August 2024
- Published online by Cambridge University Press:
- 17 September 2024, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dual formulation of constrained solutions of the multi-state Choquard equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-21
-
- Article
- Export citation