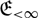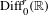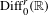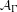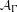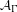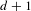Refine listing
Actions for selected content:
300 results in 37Bxx
FINITENESS OF TOPOLOGICAL ENTROPY FOR LOCALLY COMPACT ABELIAN GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 81-105
- Print publication:
- January 2021
-
- Article
- Export citation
C*-algebras of a Cantor system with finitely many minimal subsets: structures, K-theories, and the index map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1296-1341
- Print publication:
- May 2021
-
- Article
- Export citation
Automorphisms of automatic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1530-1559
- Print publication:
- May 2021
-
- Article
- Export citation
Attractors associated to a family of hyperbolic
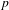 $p$ -adic plane automorphisms
$p$ -adic plane automorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1867-1882
- Print publication:
- June 2021
-
- Article
- Export citation
Entropy of general diffeomorphisms on line
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 18 February 2020, pp. 1139-1155
- Print publication:
- April 2021
-
- Article
- Export citation
Topological mixing of Weyl chamber flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 17 February 2020, pp. 1342-1368
- Print publication:
- May 2021
-
- Article
- Export citation
Lyapunov exponents for expansive homeomorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 10 February 2020, pp. 413-425
-
- Article
- Export citation
Normal amenable subgroups of the automorphism group of sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 February 2020, pp. 1250-1263
- Print publication:
- April 2021
-
- Article
- Export citation
On the virtual automorphism group of a minimal flow
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1281-1295
- Print publication:
- May 2021
-
- Article
- Export citation
Amenable uniformly recurrent subgroups and lattice embeddings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1464-1501
- Print publication:
- May 2021
-
- Article
- Export citation
A construction of subshifts and a class of semigroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 881-905
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
The expressiveness of quasiperiodic and minimal shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1086-1138
- Print publication:
- April 2021
-
- Article
- Export citation
Lower bound for the Perron–Frobenius degrees of Perron numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1264-1280
- Print publication:
- April 2021
-
- Article
- Export citation
Shadowing and structural stability for operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 961-980
- Print publication:
- April 2021
-
- Article
- Export citation
On Baire measurable colorings of group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 818-845
- Print publication:
- March 2021
-
- Article
- Export citation
The Ellis semigroup of certain constant-length substitutions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 935-960
- Print publication:
- March 2021
-
- Article
- Export citation
Frequent universality criterion and densities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 25 November 2019, pp. 846-868
- Print publication:
- March 2021
-
- Article
- Export citation
Support stability of maximizing measures for shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 09 October 2019, pp. 869-880
- Print publication:
- March 2021
-
- Article
- Export citation
Bounded complexity, mean equicontinuity and discrete spectrum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 494-533
- Print publication:
- February 2021
-
- Article
- Export citation
Topological entropy of Markov set-valued functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 24 September 2019, pp. 321-337
- Print publication:
- February 2021
-
- Article
- Export citation