A convex lattice polygon is a polygon whose vertices are points on the integer lattice and whose interior angles are strictly less than π radians. We define a(2n) to be the least possible area of a convex lattice polygon with 2n vertices. A method for constructing convex lattice polygons with area a(2n) is described, and values of a(2n) for low n are obtained.

We compare the definitions of analyticity of vector-valued functions and their connections with the topological tensor products of non-locally convex spaces.

In this note we consider Hermite-Fejér interpolation at the zeros of Jacobi polynomials and with additional boundary conditions. For the associated Hermite-Fejér type operators 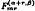and special values of α, β it was proved by the first author in recent papers that one has uniform convergence on the whole interval [−1,1]. The second author could show by introducing the concept of asymptotic positivity how to get the known convergence results for the classical Hermite-Fejér interpolation operators. In the present paper we show, using a slightly modified Bohman-Korovkin theorem for asymptotically positive functionals, that the Hermite-Fejér type interpolation polynomials 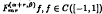, converge pointwise to f for arbitrary α, β > −1. The convergence is uniform on [−1 + δ,1 − δ].

In this paper we investigate the relationships among the notions of minimality, characteristic 0, equicontinuity, Lipschitz stability and isometry in dynamical systems. Examples are provided to show that the results obtained are sharp.

Variational inequality theory provides techniques for solving a variety of applied problems in science and engineering. Recently Noor considered some interesting general nonlinear and linear variational inequalities in a series of papers and proved the existence and uniqueness of solutions by a fixed point technique developed by Glowinski, Lions and Tremolieres and also by a fixed point technique of Lions and Stampacchia. But there are several inaccuracies in his proofs and here they have been removed and correct formulation of the theorems are stated and proved and relationships are clearly shown. The existence of solution necessitates an additional condition in one case, and less condition in the other, but uniqueness can be proved without the condition that the operator be antimonotone.

A distance is defined on the quotient of the set of submanifolds of a Euclidean space, with respect to similarity. It is then related to a previously defined function which captures the metric behaviour of paths.

The weighted Bergman space Ap, α, 0 < p < 1, a > −1 of analytic functions on the unit disc Δ in C is an F-space. We determine the dual of Ap, α explicitly.

We give conditions under which pointwise multiplication is a continuous bounded operation on kth order Sobolev-Orlicz spaces. This result is used to derive a sufficient condition under which the superposition operator is a continuous bounded operator on these spaces.

The concept of invexity is extended to nondifferentiable functions. Characterisations of nonsmooth invexity are derived as well as results in unconstrained and constrained optimisation and duality. The principal analytic tool is the generalised gradient of Clarke for Lipschitz functions.

We show that a ruled surface of finite type in a Euclidean space is a cylinder on a curve of finite type or a helicoid in Euclidean 3-space.

A number of nonoscillation criteria for the Emden-Fowler system

where a(t), b(t) > 0, r1, r2 > 0 and b(t)/a(t) is locally of bounded variation, are established employing energy function techniques. The results obtained here include many known nonoscillation theorems for the classical Emden-Fowler equations as special cases. We illustrate the results obtained with several examples.

We study in this paper the relations existing between Joly's rectangular constant (µ) and the degree of asymmetry of Birkhoff-James's orthogonality relation (β). New bounds on the variation of µ in terms of β and estimation of the values taken by β in the case of uniformly convex Banach spaces are given.

We show that if (M, g) is a distinguishing space-time, then any distance homothetic map from (M, g) onto arbitrary space-time (M′, g′) is a homothetic map; in particular, every distance preserving map is an isometry.

Interior estimates are derived for the C2, µ-Hölder norm of the radius vector X ∈ C1, 1 (Ω) of a locally convex surface Σ in terms of the first fundamental form IΣ, the Gauss curvature K and the integral ∫ |H| dσ. Here H is the mean curvature of Σ. The coefficients gij of IΣ are assumed to belong to the Hölder class C2, µ (Ω) for some μ, 0 < μ < 1. A boundary condition is discussed which ensures an estimate for ∫ | H | dσ.

The Wielandt subgroup is the intersection of the normalisers of all the subnormal subgroups of a group. For a finite group it is a non-trivial characteristic subgroup, and this makes it possible to define an ascending normal series terminating at the group. This series is called the Wielandt series and its length determines the Wielandt length of the group. In this paper the Wielandt subgroup of a metacyclic p–group is identified, and using this information it is shown that if a metacyclic p–group has Wielandt length n, its nilpotency class is n or n + 1.

Some properties of the Hausdorff distance in complete metric spaces are discussed. Results obtained in this paper explain ideas used in the theory of measures of noncompactness.

In this paper, the topology of the Denjoy space and characterisation of precompact sets in the Denjoy space are given.

An associative ring R with identity is called a PS-ring if soc(RR) is projective. We construct a non- PS-ring R which is a subdirect product of two PS-rings, thus answering a question of Nicholson and Watters in the negative.