It is well-known that the approximation to f(x) ∈ C2π, by nth trigonometric Lagrange interpolating polynomials with equally spaced nodes in C2π, has an upper bound In(n)En(f), where En(f) is the nth best approximation of f(x). For various natural reasons, one can ask what might happen in Lp space? The present paper indicates that the result about the trigonometric Lagrange interoplating approximation in Lp space for 1 < p < ∞ may be “bad” to an arbitrary degree.

A study is made of the minimum number of generators of the n-th direct power of certain finitely generated groups.

I discussed the sort of thing Bernhard had in mind concerning the BFC-problem in [3], an article written for his sixieth birthday. This vigesennial contribution deals with one of the “and others”, namely the zero deficiency problem. in his article [1] bearing the same title as this one, Bernhard gave 2-generator 2-relator presentations of some metacyclic groups; if one distils and formalises the process used there, one gets the following result, to be used later in constructing some zero-deficiency finite p-groups.

Let G be a locally compact abelian group, with character group Ĝ. Let ψ be an arbitrary continuous real-valued homomorphism defined on Ĝ. For f in LP(G), 1 < p ≤ 2, let

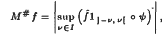
where 1[−ν, ν] is the indicator function of the interval [ − ν, ν ], and I is an unbounded increasing sequence of positive real numbers. Then there is a constant Mp, independent of f, such that ‖M#f‖p ≤ Mp ‖f‖p. Consequently, the pointwise limit of the function 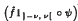exists, almost everywhere on G, as ν tends to infinity. Using this result and a generalised version of Riesz's theorem on conjugate functions, we obtain a pointwise inversion for Fourier transforms of functions on Ra × Tb, where a and b are nonnegative integers, and on various other locally compact abelian groups.

A consideration of the separation properties of pre-neighbourhood lattices, leads to the definition and characterisation of T1-neighbourhood lattices in terms of the properties of the neighbourhood mapping, independently of points. It is then shown that if net convergence is defined in neighbourhood lattices as a consequence of replacing ‘point’ by ‘set’ in topological convergence, then the limits of convergent nets are unique. The relationship between continuity and convergence is established with the proof of the statement that a residuated function between conditionally complete T1-neighbourhood lattices is continuous if and only if it preserves the limit of convergent nets. If P(X) denotes the power set of X, then the observation that a filter in a topological space (X, T) is a net in P(X) leads to a discussion of the net convergence of a filter as a special case of net convergence. Particular attention is paid to maximal filters, Fréchet filters and to the filter generated by the limit elements of a net. Further, if the ‘filter’ convergence of a filter F in a topological space (X, T) is given by , if η(x) ⊆ F, then the relationship between ‘filter’ convergence and the net convergence of a filter in P(X) is established. Finally, it is proved that, in the neighbourhood system ‘lifted’ from a topological space to P(P(X)), the continuous image of a filter which converges to a singleton set is a convergent filter with the appropriate image set as the limit.

The concept of kth Hölderian functions on an interval [a, b] which generalises the notion of Hölderian (Lipschitzian) functions of positive order on [a, b] is introduced. The relationship of such functions to functions of bounded kth variation and absolutely kth continuous functions is examined. Properties induced by higher order derivatives in this new class of functions are investigated.

For a triple (M, H,ξ0) of a von Neumann algebra M on a Hilbert space H with a cyclic and separating vector ξ0, every order isormorphism ø, of H such that øξ0 = ξ0 is an orthogonal decomposition isomorphism if and only if ξ0 is a trace vector.

Let f(z) be a n-valued algebroid function of order λ(0 ≤ λ ≤ 1), Sato obtained an elliptic theorem for f(z) with a condition. In this paper, we prove that Sato's theorem is true without conditions and give a generalisation.

Plücker formulae for horizontal curves in SO(m)-flag manifolds are derived. These formulae are seen to generalise the usual Plücker formulae for projective space curves. They also have applications in the theory of minimal surfaces in Euclidean sphere and the complex hyperquadric.

We prove that the simply connected compact mixed foliate CR-submanifold in a hyperbolic complex space form is either a complex submanifold or a totally real submanifold. This is the problem posed by Chen.

We prove the Legendre Necessary Condition of the Calculus of Variations in Mean an arbitrary finite dimension. When the Lagrangian is convex, we establish that if the Euler-Lagrange equation possesses an almost periodic solution then it possesses periodic and constant solutions. We deduce from this fact various consequences on the structure of the set of almost periodic solutions.

In this paper we consider the error estimates for some boundary-flux calculation procedures applied to two-point semilinear and strongly nonlinear elliptic boundary value problems. The case of semilinear parabolic problems is also studied. We prove that the computed flux is superconvergent with second and third order of convergence for linear and quadratic elements respectively. Corresponding estimates for higher order elements may also be obtained by following the general line of argument.

Huq presented a general study of semi-homomorphisms of rings, following, amongst others, Kaplansky's study of semi-automorphisnis of rings and Herstein's study of semi-homomorphisms of groups. Huq gave several “sufficient” conditions for a semi-homomorphism and a semi-monomorphism of rings to be a homomorphism and a monomorphism respectively. In this note we introduce semi-subgroups of groups, provide counterexamples to four of Huq's assertions and show how a minor, albeit forced, change to one of the conditions of the fourth assertion turns it into a special case of another theorem of Huq's.

The author would like to correct an error in the statement of a result ‘in Bull. Aust. Math. Soc. 36 (1987) 485–492’ and also to incorporate an additional result.