Contents
Research Article
Baire Category And Laurent Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 824-830
-
- Article
-
- You have access
- Export citation
Rings Characterized by their Cyclic Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-111
-
- Article
-
- You have access
- Export citation
Solvable Subgroups and their Lie Algebras in Characteristic p
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 308-311
-
- Article
-
- You have access
- Export citation
Characterizations of Vitali Conditions with Overlap in Terms of Convergence of Classes of Amarts
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1033-1046
-
- Article
-
- You have access
- Export citation
Infinite Systems of Differential Equations II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 596-603
-
- Article
-
- You have access
- Export citation
Simple Algebras Over Rational Function Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 831-835
-
- Article
-
- You have access
- Export citation
Quotients and Inverse Limits of Spaces of Orderings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 604-616
-
- Article
-
- You have access
- Export citation
Quadratic forms over Quadratic Extensions of Fields with Two Quaternion Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1047-1058
-
- Article
-
- You have access
- Export citation
An Alternative Approach to Laguerre Polynomial Identities in Combinatorics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-319
-
- Article
-
- You have access
- Export citation
Coinitial Grapfis and Whitehead Automorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 112-123
-
- Article
-
- You have access
- Export citation
Quelques Propriétés Sur Le Normalisateur D'un Pseudogroupe De Lie Transitif
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 124-129
-
- Article
-
- You have access
- Export citation
Classification of Finite Spaces of Orderings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-330
-
- Article
-
- You have access
- Export citation
Partial λ-Geometries and Generalized Hadamard Matrices Over Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 617-627
-
- Article
-
- You have access
- Export citation
Tensor Products of Holomorphic Discrete Series Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 836-844
-
- Article
-
- You have access
- Export citation
Dispersed Factorization Structures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1059-1071
-
- Article
-
- You have access
- Export citation
On a Uniqueness Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1072-1076
-
- Article
-
- You have access
- Export citation
Embedding Smooth Dendroids in Hyperspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-138
-
- Article
-
- You have access
- Export citation
On the Operator Identity ∑ AkXBk ≡ 0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 845-857
-
- Article
-
- You have access
- Export citation
A Generalization of Uniformly Rotund Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 628-636
-
- Article
-
- You have access
- Export citation
The Unrestricted Section Properties of Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 331-336
-
- Article
-
- You have access
- Export citation
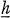 denotes the Lie algebra of
denotes the Lie algebra of  is the Lie algebra
is the Lie algebra 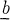 of some Borel subgroup
of some Borel subgroup 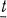 of some maximal torus
of some maximal torus 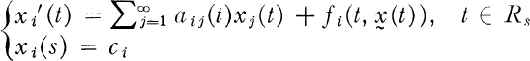
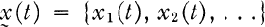 denotes a sequence-valued function. Conditions on the coefficient matrix
denotes a sequence-valued function. Conditions on the coefficient matrix 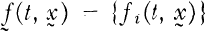 were established which guarantee that for each initial value
were established which guarantee that for each initial value 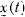 is continuous and
is continuous and 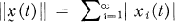 converges uniformly on compact subsets of
converges uniformly on compact subsets of 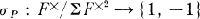
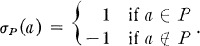
 .
.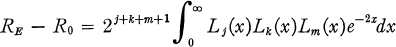
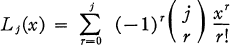
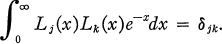
 is a set of
is a set of 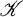 form a useful categorical tool. As is known, any
form a useful categorical tool. As is known, any 
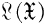 , the algebra of bounded operators on ᚕ, defined by
, the algebra of bounded operators on ᚕ, defined by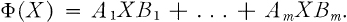

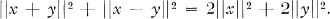
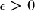

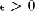 0 we have
0 we have 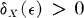 .
.