Contents
Research Article
Lie Algebras with Nilpotent Centralizers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 929-941
-
- Article
-
- You have access
- Export citation
Projections on Bergman Spaces Over Plane Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1269-1280
-
- Article
-
- You have access
- Export citation
On Counting Types of Symmetries in Finite Unitary Reflection Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 252-254
-
- Article
-
- You have access
- Export citation
A Theory of Uniformities for Generalized Ordered Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 35-44
-
- Article
-
- You have access
- Export citation
A Remark on Disintegrations With Almost All Components Non
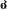 -Additive
-Additive
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 786-788
-
- Article
-
- You have access
- Export citation
Fourier Transforms of Unbounded Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1281-1292
-
- Article
-
- You have access
- Export citation
On Global Inverse Theorems of Szász and Baskakov Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 255-263
-
- Article
-
- You have access
- Export citation
Sequence Enumeration and the de Bruijn-Van Aardenne Ehrenfest-Smith-Tutte Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 488-495
-
- Article
-
- You have access
- Export citation
The Asymptotic Behaviour of Equidistant Permutation Arrays
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 45-48
-
- Article
-
- You have access
- Export citation
Almost Split Sequences whose Middle Term has at most Two Indecomposable Summands
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 942-960
-
- Article
-
- You have access
- Export citation
Criteres de G-Stabilite en Termes de Transversalite
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 264-273
-
- Article
-
- You have access
- Export citation
Polynomial Approximation and Growth of Generalized Axisymmetrig Potentials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-59
-
- Article
-
- You have access
- Export citation
Block-Finite Orthomodular Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-985
-
- Article
-
- You have access
- Export citation
Local Spaces with Three Cells as H-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1293-1306
-
- Article
-
- You have access
- Export citation
Sur La Classification Des Symetries Des C*-Algebres UHF
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 496-523
-
- Article
-
- You have access
- Export citation
Noether Lattices Representable as Quotients of the Lattice of Monomially Generated Ideals of Polynomial Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 789-799
-
- Article
-
- You have access
- Export citation
On Certain Polynomials of Gaussian Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 274-281
-
- Article
-
- You have access
- Export citation
Labeled Bipartite Blocks
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 60-68
-
- Article
-
- You have access
- Export citation
Bounding the Valency of Polygonal Graphs With Odd Girth
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1307-1321
-
- Article
-
- You have access
- Export citation
Combinatorial Oriented Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 986-1004
-
- Article
-
- You have access
- Export citation

 be the Bergman kernel of
be the Bergman kernel of 
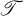 )
)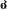 -Additive
-Additive
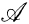 ,
,  a sub σ-algebra of
a sub σ-algebra of 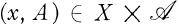 is called a
is called a 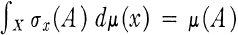
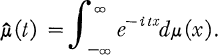
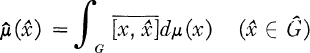
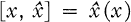 One answer to the question “Which functions can be represented as Fourier transforms of bounded measures?” was given by the following criterion due to Schoenberg [
One answer to the question “Which functions can be represented as Fourier transforms of bounded measures?” was given by the following criterion due to Schoenberg [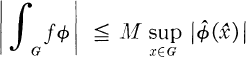
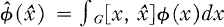
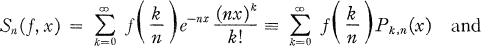
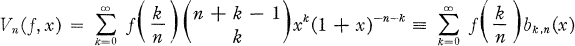
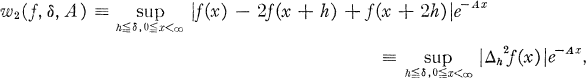
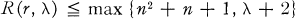
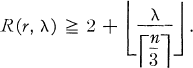
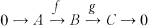 in mod A is said to be
in mod A is said to be 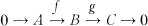 [
[ l'anneau des germes en 0 des fonctions numériques de classe
l'anneau des germes en 0 des fonctions numériques de classe  de la structure de groupe définie par la multiplication:
de la structure de groupe définie par la multiplication:
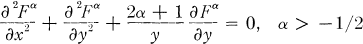
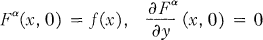
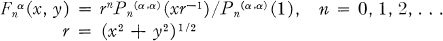
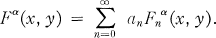
 une symétrie de
une symétrie de  ; on associe à θ un entier généralisé
; on associe à θ un entier généralisé  (
(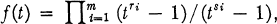
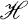 ,
, 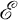 ) consisting of a graph
) consisting of a graph