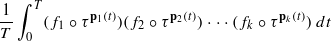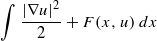Contents
Research Article
Deterministic and stochastic perturbations of area preserving flows on a two-dimensional torus
-
- Published online by Cambridge University Press:
- 05 April 2011, pp. 899-918
-
- Article
- Export citation
Complex dynamics of Möbius semigroups
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 1889-1929
-
- Article
- Export citation
The structure of the C*-algebra of a locally injective surjection
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 1226-1248
-
- Article
- Export citation
A Garden of Eden theorem for linear subshifts
-
- Published online by Cambridge University Press:
- 13 June 2011, pp. 81-102
-
- Article
- Export citation
A canonical thickening of ℚ and the entropy of α-continued fraction transformations
-
- Published online by Cambridge University Press:
- 14 September 2011, pp. 1249-1269
-
- Article
- Export citation
Dynamics of non-classical interval exchanges
-
- Published online by Cambridge University Press:
- 08 November 2011, pp. 1930-1971
-
- Article
- Export citation
Residually finite actions and crossed products
-
- Published online by Cambridge University Press:
- 17 October 2011, pp. 1585-1614
-
- Article
- Export citation
Computing the critical dimensions of Bratteli–Vershik systems with multiple edges
-
- Published online by Cambridge University Press:
- 05 April 2011, pp. 103-117
-
- Article
- Export citation
Co-induction in dynamical systems
-
- Published online by Cambridge University Press:
- 24 May 2011, pp. 919-940
-
- Article
- Export citation
Norm convergence of continuous-time polynomial multiple ergodic averages
-
- Published online by Cambridge University Press:
- 21 October 2011, pp. 361-382
-
- Article
- Export citation
From discrete- to continuous-time ergodic theorems
-
- Published online by Cambridge University Press:
- 16 December 2011, pp. 383-426
-
- Article
- Export citation
Entropy, Lyapunov exponents and escape rates in open systems
-
- Published online by Cambridge University Press:
- 06 September 2011, pp. 1270-1301
-
- Article
- Export citation
On notions of determinism in topological dynamics
-
- Published online by Cambridge University Press:
- 06 September 2011, pp. 119-140
-
- Article
- Export citation
On the self-similarity problem for smooth flows on orientable surfaces
-
- Published online by Cambridge University Press:
- 16 September 2011, pp. 1615-1660
-
- Article
- Export citation
On Arnol’d’s and Kazhdan’s equidistribution problems
-
- Published online by Cambridge University Press:
- 23 November 2011, pp. 1972-1990
-
- Article
- Export citation
Invariant rigid geometric structures and expanding maps
-
- Published online by Cambridge University Press:
- 06 May 2011, pp. 941-959
-
- Article
- Export citation
Some results on minimizers and stable solutions of a variational problem
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 1302-1312
-
- Article
- Export citation
On weak mixing, minimality and weak disjointness of all iterates
-
- Published online by Cambridge University Press:
- 14 October 2011, pp. 1661-1672
-
- Article
- Export citation
Positive entropy invariant measures on the space of lattices with escape of mass
-
- Published online by Cambridge University Press:
- 27 January 2011, pp. 141-157
-
- Article
- Export citation
Sofic entropy and amenable groups
-
- Published online by Cambridge University Press:
- 13 June 2011, pp. 427-466
-
- Article
- Export citation