Contents
Research Article
Large semigroups of cellular automata
-
- Published online by Cambridge University Press:
- 20 October 2011, pp. 1991-2010
-
- Article
- Export citation
Escape rates for Gibbs measures
-
- Published online by Cambridge University Press:
- 27 April 2011, pp. 961-988
-
- Article
-
- You have access
- Export citation
Circle diffeomorphisms forced by expanding circle maps
-
- Published online by Cambridge University Press:
- 01 November 2011, pp. 2011-2024
-
- Article
- Export citation
A Cr unimodal map with an arbitrary fast growth of the number of periodic points
-
- Published online by Cambridge University Press:
- 19 April 2011, pp. 159-165
-
- Article
- Export citation
Strong renewal theorems and Lyapunov spectra for α-Farey and α-Lüroth systems
-
- Published online by Cambridge University Press:
- 02 September 2011, pp. 989-1017
-
- Article
- Export citation
Recurrence and ergodicity of random walks on linear groups and on homogeneous spaces
-
- Published online by Cambridge University Press:
- 14 June 2011, pp. 1313-1349
-
- Article
- Export citation
Bounded cohomology and totally real subspaces in complex hyperbolic geometry
-
- Published online by Cambridge University Press:
- 14 September 2011, pp. 467-478
-
- Article
- Export citation
Dynamical properties of the negative beta-transformation
-
- Published online by Cambridge University Press:
- 14 October 2011, pp. 1673-1690
-
- Article
- Export citation
There is no minimal action of ℤ2 on the plane
-
- Published online by Cambridge University Press:
- 05 April 2011, pp. 167-172
-
- Article
- Export citation
Spatial determinism for a free Z2-action
-
- Published online by Cambridge University Press:
- 16 December 2011, pp. 479-489
-
- Article
- Export citation
Rigidity and absence of line fields for meromorphic and Ahlfors islands maps
-
- Published online by Cambridge University Press:
- 23 November 2011, pp. 1691-1710
-
- Article
- Export citation
Carrots for dessert
-
- Published online by Cambridge University Press:
- 17 November 2011, pp. 2025-2055
-
- Article
- Export citation
On weak KAM theory for N-body problems
-
- Published online by Cambridge University Press:
- 27 April 2011, pp. 1019-1041
-
- Article
- Export citation
Differentiating potential functions of SRB measures on hyperbolic attractors
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 1350-1369
-
- Article
- Export citation
Subsemigroups of transitive semigroups
-
- Published online by Cambridge University Press:
- 24 May 2011, pp. 1043-1071
-
- Article
- Export citation
On recurrence and ergodicity for geodesic flows on non-compact periodic polygonal surfaces
-
- Published online by Cambridge University Press:
- 18 January 2012, pp. 491-515
-
- Article
- Export citation
Density of hyperbolicity for rational maps with Cantor Julia sets
-
- Published online by Cambridge University Press:
- 08 September 2011, pp. 1711-1726
-
- Article
- Export citation
On the distribution of orbits of geometrically finite hyperbolic groups on the boundary
-
- Published online by Cambridge University Press:
- 05 April 2011, pp. 173-189
-
- Article
- Export citation
Ring and module structures on dimension groups associated with a shift of finite type
-
- Published online by Cambridge University Press:
- 01 June 2012, pp. 1370-1399
-
- Article
- Export citation
Towards a semi-local study of parabolic invariant curves for fibered holomorphic maps
-
- Published online by Cambridge University Press:
- 14 October 2011, pp. 2056-2070
-
- Article
- Export citation
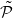 such that the
such that the 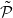 -names of an arbitrarily small one-sided cone determine the points.
-names of an arbitrarily small one-sided cone determine the points.