Contents
Research Article
On the critical dimensions of product odometers
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 475-485
-
- Article
- Export citation
The Lyapunov spectrum of some parabolic systems
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 919-940
-
- Article
- Export citation
Overlapping self-affine sets of Kakeya type
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 941-965
-
- Article
- Export citation
Subdiffusive behavior generated by irrational rotations
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1217-1233
-
- Article
- Export citation
Birkhoff normalization and superintegrability of Hamiltonian systems
-
- Published online by Cambridge University Press:
- 02 March 2009, pp. 1853-1880
-
- Article
- Export citation
Category theorems for stable semigroups
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 487-494
-
- Article
- Export citation
Transitivity of Euclidean-type extensions of hyperbolic systems
-
- Published online by Cambridge University Press:
- 03 February 2009, pp. 1585-1602
-
- Article
- Export citation
Robustly expansive codimension-one homoclinic classes are hyperbolic
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 179-200
-
- Article
- Export citation
A family of entire functions with Baker domains
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 495-514
-
- Article
- Export citation
Natural invariant measures, divergence points and dimension in one-dimensional holomorphic dynamics
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1235-1255
-
- Article
- Export citation
Global attractors of analytic plane flows
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 967-981
-
- Article
- Export citation
The Mañé–Conze–Guivarc’h lemma for intermittent maps of the circle
-
- Published online by Cambridge University Press:
- 03 February 2009, pp. 1603-1611
-
- Article
- Export citation
Resonance between Cantor sets
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 201-221
-
- Article
- Export citation
Continuity of the Lyapunov exponent for analytic quasiperiodic cocycles
-
- Published online by Cambridge University Press:
- 30 September 2009, pp. 1881-1905
-
- Article
- Export citation
A family of 2-graphs arising from two-dimensional subshifts
-
- Published online by Cambridge University Press:
- 12 March 2009, pp. 1613-1639
-
- Article
- Export citation
An asymptotic-numerical approach for examining global solutions to an ordinary differential equation
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 223-253
-
- Article
- Export citation
A quantitative mean ergodic theorem for uniformly convex Banach spaces
-
- Published online by Cambridge University Press:
- 17 March 2009, pp. 1907-1915
-
- Article
- Export citation
Parameter rays in the space of exponential maps
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 515-544
-
- Article
- Export citation
Open maps between shift spaces
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1257-1272
-
- Article
- Export citation
Finite blocking property versus pure periodicity
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 983-996
-
- Article
- Export citation
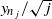 is asymptotically normally distributed. For
is asymptotically normally distributed. For 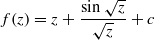
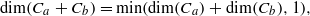
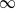 . These parameters are organized in curves in parameter space called
. These parameters are organized in curves in parameter space called