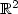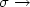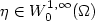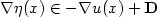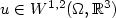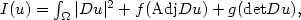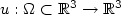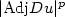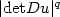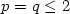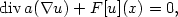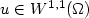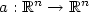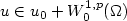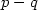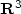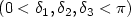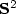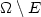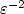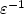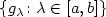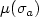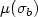Refine listing
Actions for selected content:
Contents
Research Article
The Lazy Travelling Salesman Problem in $\mathbb{R}^2$
-
- Published online by Cambridge University Press:
- 20 June 2007, pp. 538-552
-
- Article
- Export citation
On the existence of variations, possibly with pointwise gradient constraints
-
- Published online by Cambridge University Press:
- 12 May 2007, pp. 331-342
-
- Article
- Export citation
Model problems from nonlinear elasticity:partial regularity results
-
- Published online by Cambridge University Press:
- 14 February 2007, pp. 120-134
-
- Article
- Export citation
Local Lipschitz continuity of solutions of non-linear elliptic differential-functional equations
-
- Published online by Cambridge University Press:
- 20 July 2007, pp. 707-716
-
- Article
- Export citation
Existence and regularity of minimizers of nonconvex integrals with p-q growth
-
- Published online by Cambridge University Press:
- 12 May 2007, pp. 343-358
-
- Article
- Export citation
Non-local approximation of free-discontinuity problemswith linear growth
-
- Published online by Cambridge University Press:
- 14 February 2007, pp. 135-162
-
- Article
- Export citation
Numerical study of a new global minimizerfor the Mumford-Shah functional in R3
-
- Published online by Cambridge University Press:
- 20 June 2007, pp. 553-569
-
- Article
- Export citation
A relaxation result for energies defined on pairs set-function and applications
-
- Published online by Cambridge University Press:
- 20 July 2007, pp. 717-734
-
- Article
- Export citation
Homogenization of periodic non self-adjoint problemswith large drift and potential
-
- Published online by Cambridge University Press:
- 20 July 2007, pp. 735-749
-
- Article
- Export citation
Conformal mapping and inverse conductivity problem withone measurement
-
- Published online by Cambridge University Press:
- 14 February 2007, pp. 163-177
-
- Article
- Export citation
The formation of a tree leaf
-
- Published online by Cambridge University Press:
- 12 May 2007, pp. 359-377
-
- Article
- Export citation
Stabilization of Schrödinger equation in exterior domains
-
- Published online by Cambridge University Press:
- 20 June 2007, pp. 570-579
-
- Article
- Export citation
Optimal control of a stochastic heat equationwith boundary-noise and boundary-control
-
- Published online by Cambridge University Press:
- 14 February 2007, pp. 178-205
-
- Article
- Export citation
Second-order sufficient optimality conditionsfor a semilinear optimal control problem with nonlocal radiation interface conditions
-
- Published online by Cambridge University Press:
- 20 July 2007, pp. 750-775
-
- Article
- Export citation
New Farkas-type constraintqualificationsin convex infinite programming
-
- Published online by Cambridge University Press:
- 20 June 2007, pp. 580-597
-
- Article
- Export citation
Hamiltonian identification for quantum systems: well-posedness and numerical approaches
-
- Published online by Cambridge University Press:
- 12 May 2007, pp. 378-395
-
- Article
- Export citation
On the well-posedness and regularity of the waveequation with variable coefficients
-
- Published online by Cambridge University Press:
- 05 September 2007, pp. 776-792
-
- Article
- Export citation
Morse index and bifurcation of p-geodesics on semi Riemannian manifolds
-
- Published online by Cambridge University Press:
- 26 July 2007, pp. 598-621
-
- Article
- Export citation
A relaxation result in BV for integral functionalswith discontinuous integrands
-
- Published online by Cambridge University Press:
- 12 May 2007, pp. 396-412
-
- Article
- Export citation
Correction
Regularity and variationality of solutionsto Hamilton-Jacobi equations. Part I: Regularity (errata)
-
- Published online by Cambridge University Press:
- 12 May 2007, pp. 413-417
-
- Article
- Export citation