Volume 5 - 2025
Latest volume of Flow
Contents
Research Article
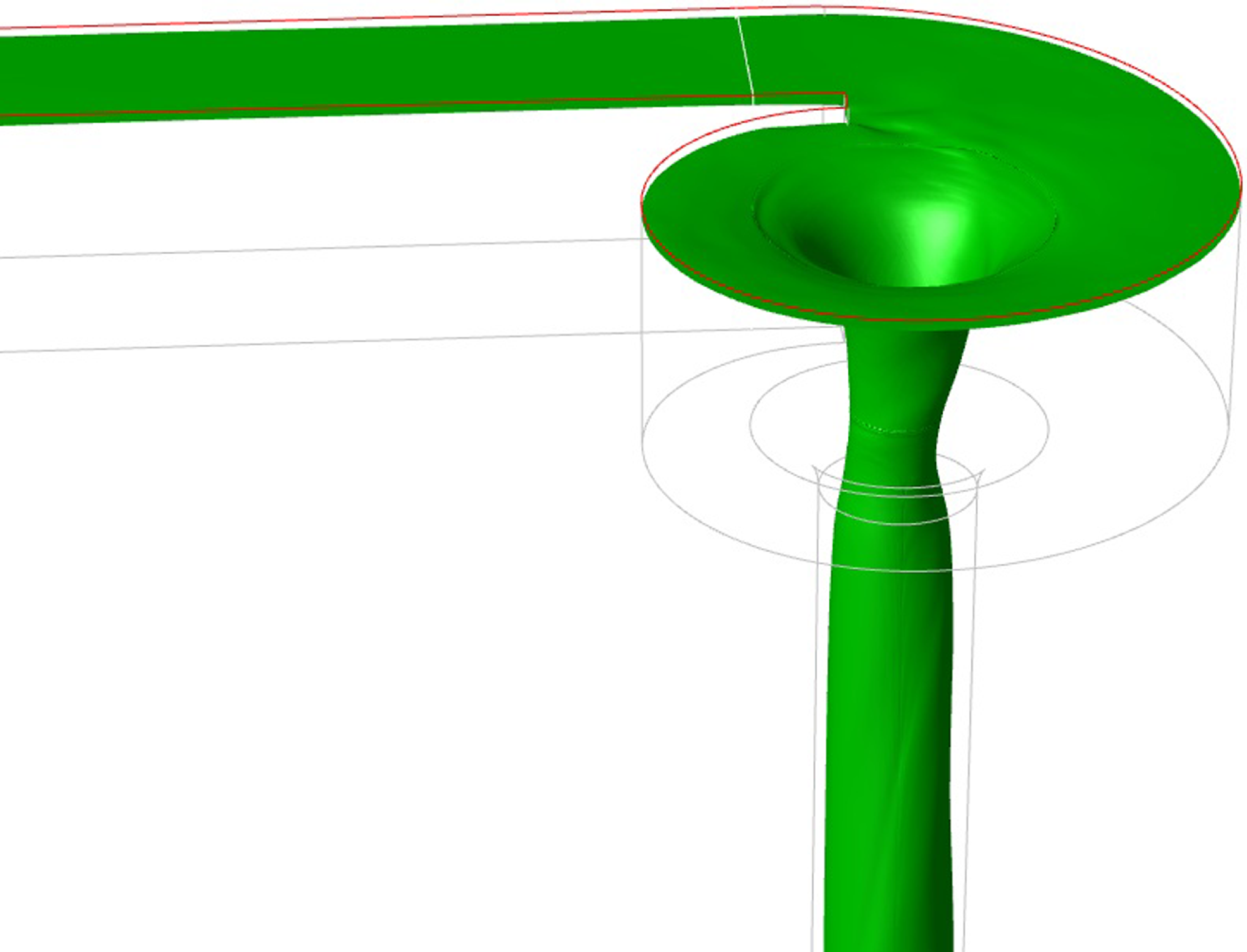
Transition mechanisms in hypersonic wind-tunnel nozzles: a methodological approach using global linear stability analysis
-
- Published online by Cambridge University Press:
- 05 December 2025, E42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of turbulent flow over mobile dune
-
- Published online by Cambridge University Press:
- 27 November 2025, E41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large language model driven development of turbulence models
-
- Published online by Cambridge University Press:
- 21 November 2025, E40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enhanced flow rate prediction of disturbed pipe flow using a shallow neural network
-
- Published online by Cambridge University Press:
- 06 November 2025, E39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
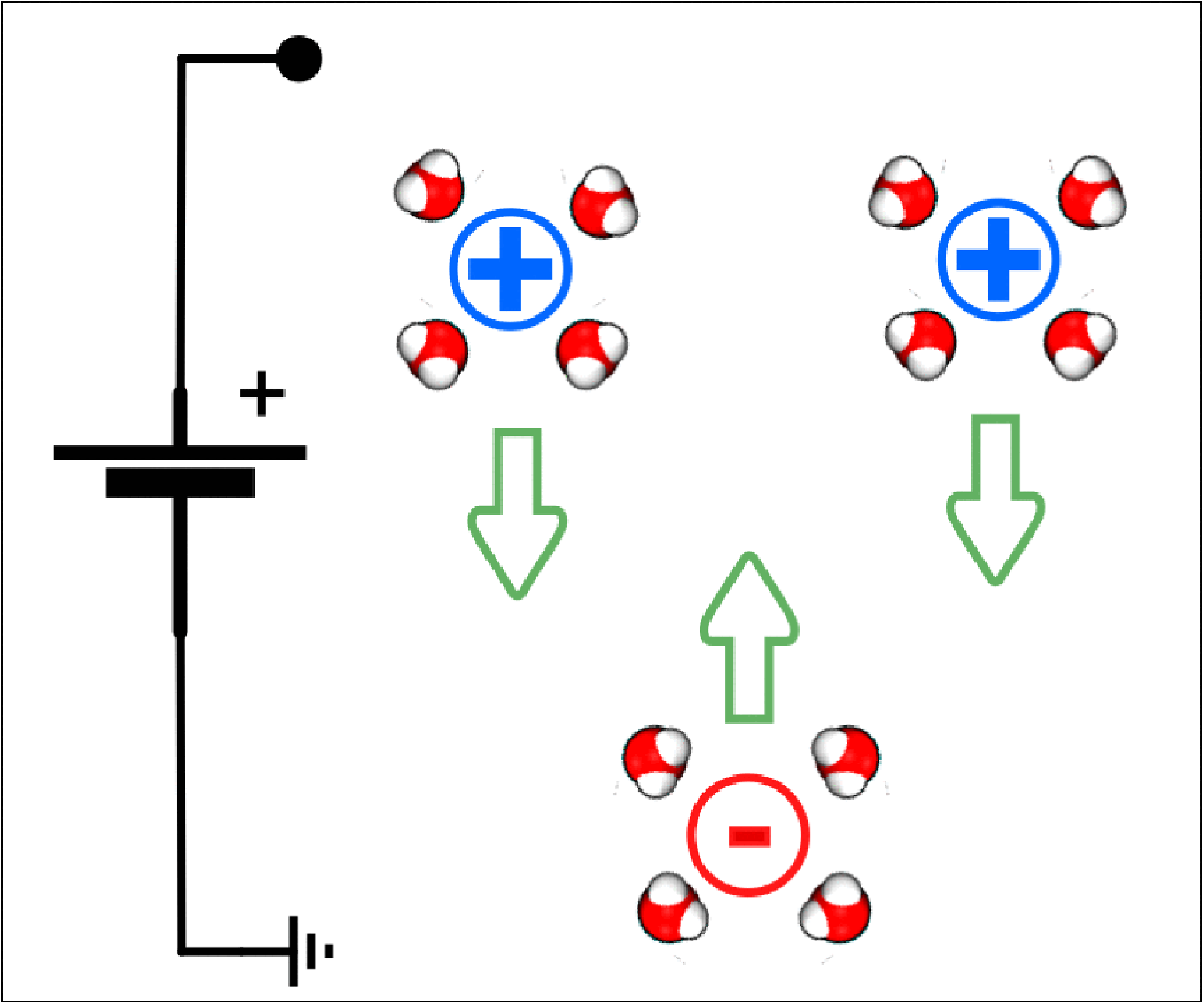
Unveiling mysteries of micro-porous structures in xylem vascular of plants: characterising nutrient transport using electro-hydrodynamics
-
- Published online by Cambridge University Press:
- 03 November 2025, E38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How a table modulates the risk of airborne transmission between facing individuals
-
- Published online by Cambridge University Press:
- 03 November 2025, E37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental and numerical flow field study of submerged translating impinging inclined water jets
-
- Published online by Cambridge University Press:
- 16 October 2025, E36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tip leakage flow structure and cavitation inception in a ducted marine propeller
-
- Published online by Cambridge University Press:
- 13 October 2025, E35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
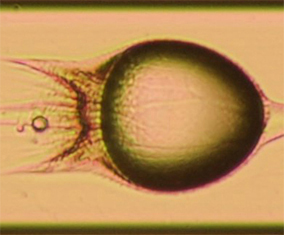
Dynamics of droplet formation in rotary flow focusing
-
- Published online by Cambridge University Press:
- 30 September 2025, E34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall shear stress generated by a Bernoulli pad: experiments and numerical simulations
-
- Published online by Cambridge University Press:
- 29 September 2025, E33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Performance of a two-body wave energy converter with an annular heave plate
-
- Published online by Cambridge University Press:
- 22 September 2025, E32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Demystifying the discharge coefficient for flow over thin weirs and sills
-
- Published online by Cambridge University Press:
- 08 August 2025, E31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluid dynamics in the vitreous chamber during infusion in ophthalmic surgery: a numerical study
-
- Published online by Cambridge University Press:
- 28 July 2025, E30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large eddy simulations of transient flow characteristics in a drop shaft with a scroll vortex intake
-
- Published online by Cambridge University Press:
- 10 July 2025, E29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Validity of approximated expressions for electro-osmotic flow in nanopores evaluated by continuum electrohydrodynamics and atomistic simulations
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2025, E28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
Turbulent boundary layer development over an air cavity – ERRATUM
-
- Published online by Cambridge University Press:
- 10 July 2025, E27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
Hopper flows of dense suspensions: a 2D microfluidic model system
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2025, E26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symbolic regression modelling of the linear growth rates of stationary cross-flow instabilities
-
- Published online by Cambridge University Press:
- 19 June 2025, E25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Formation of microfluidic droplets and jets in a solvent-rich oil phase
- Part of:
-
- Published online by Cambridge University Press:
- 02 July 2025, E24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evaluating the power mean method to determine an equivalent sandgrain roughness parameter over streamwise-heterogeneous roughness
-
- Published online by Cambridge University Press:
- 17 June 2025, E23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation