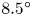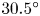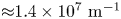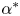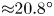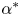Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 5
Oblique collisions of internal wave beams and associated resonances
-
- Published online by Cambridge University Press:
- 19 September 2012, pp. 337-363
-
- Article
- Export citation
- Cited by 5
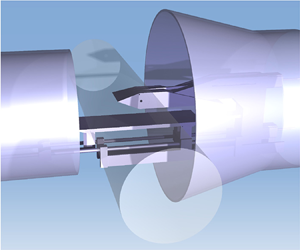
A Stokesian analysis of a submerged viscous jet impinging on a planar wall
-
- Published online by Cambridge University Press:
- 28 September 2012, pp. 531-551
-
- Article
- Export citation
- Cited by 5
Helicity generation and vorticity dynamics in helically symmetric flow
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 125-149
-
- Article
- Export citation
- Cited by 5
Dissipative descent: rocking and rolling down an incline
-
- Published online by Cambridge University Press:
- 15 October 2007, pp. 295-318
-
- Article
- Export citation
- Cited by 5
Stable and unstable supersonic stagnation of an axisymmetric rotating magnetized plasma
-
- Published online by Cambridge University Press:
- 15 February 2022, A35
-
- Article
- Export citation
- Cited by 5
Pressure plateau of separation induced by shock impingement in a Mach 5 flow
-
- Published online by Cambridge University Press:
- 26 September 2023, R1
-
- Article
- Export citation
- Cited by 5
Particle–particle drag force in inertial bidisperse gas–particle suspensions
-
- Published online by Cambridge University Press:
- 23 November 2022, A11
-
- Article
- Export citation
- Cited by 5
Turbulence modulation by charged inertial particles in channel flow
-
- Published online by Cambridge University Press:
- 12 August 2024, A2
-
- Article
- Export citation
- Cited by 5
On shock induced aerobreakup of a wall-attached droplet
-
- Published online by Cambridge University Press:
- 25 September 2023, A31
-
- Article
- Export citation
- Cited by 5
Prediction of the phase difference between large-scale velocity and Reynolds stress fluctuations in wall turbulence
-
- Published online by Cambridge University Press:
- 14 August 2023, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 5
Oscillating line source in a shear flow with a free surface: critical layer-like contributions
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 201-231
-
- Article
- Export citation
- Cited by 5
Longitudinal wall motion during peristalsis and its effect on reflux
-
- Published online by Cambridge University Press:
- 01 June 2023, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 5
The Cauchy–Poisson problem for a rotating liquid
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 75-88
-
- Article
- Export citation
- Cited by 5
Inertial-particle accelerations in turbulence: a Lagrangian closure
-
- Published online by Cambridge University Press:
- 31 May 2016, pp. 187-200
-
- Article
- Export citation
- Cited by 5
Steady streaming confined between three-dimensional wavy surfaces
-
- Published online by Cambridge University Press:
- 03 August 2010, pp. 430-455
-
- Article
- Export citation
- Cited by 5
Unsteady laminar boundary layer along the symmetry plane of an impulsively started prolate spheroid
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 413-435
-
- Article
- Export citation
- Cited by 5
New bounds on the vertical heat transport for Bénard–Marangoni convection at infinite Prandtl number
-
- Published online by Cambridge University Press:
- 27 December 2019, R4
-
- Article
- Export citation
- Cited by 5
Nonlinearity of the three-dimensional flow past a flat blunt ship
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 345-361
-
- Article
- Export citation
- Cited by 5
Second-order supercavitating hydrofoil theory
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 321-332
-
- Article
- Export citation
- Cited by 5
On Richtmyer–Meshkov finger collisions in a light fluid layer under reshock conditions
-
- Published online by Cambridge University Press:
- 02 December 2024, A87
-
- Article
- Export citation
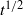 , a behaviour akin to that of forced waves at cut-off frequencies.
, a behaviour akin to that of forced waves at cut-off frequencies.