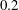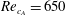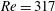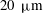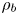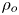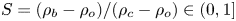Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2
Effect of wall suction on rotating disk absolute instability
-
- Published online by Cambridge University Press:
- 24 February 2016, pp. 704-737
-
- Article
- Export citation
- Cited by 2
The fluid mechanics of active flow control at very large scales
-
- Published online by Cambridge University Press:
- 22 November 2024, F9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
On symmetric intrusions in a linearly stratified ambient: a revisit of Benjamin's steady-state propagation results
-
- Published online by Cambridge University Press:
- 19 October 2021, A8
-
- Article
- Export citation
- Cited by 2
Universal behaviour in boundary-driven electrokinetic flows
-
- Published online by Cambridge University Press:
- 08 May 2025, A50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Interfacial dynamics of a confined liquid–vapour bilayer undergoing evaporation
-
- Published online by Cambridge University Press:
- 15 October 2018, pp. 1-37
-
- Article
- Export citation
- Cited by 2
Saturation of flames to multiple inputs at one frequency
-
- Published online by Cambridge University Press:
- 12 December 2023, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
A series of two-phase models for grain–fluid flows with dilatancy
-
- Published online by Cambridge University Press:
- 04 April 2025, A43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Exotic wakes of an oscillating circular cylinder: how singles pair up
-
- Published online by Cambridge University Press:
- 06 July 2021, F1
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 2
Nonlinear dynamics of unstably stratified two-layer shear flow in a horizontal channel
-
- Published online by Cambridge University Press:
- 18 January 2023, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Dispersive mixing: within or between pores?
-
- Published online by Cambridge University Press:
- 12 March 2025, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Biomimetics and cilia propulsion
-
- Published online by Cambridge University Press:
- 17 June 2011, pp. 1-4
-
- Article
-
- You have access
- Export citation
- Cited by 2
Finite Froude and Rossby numbers counter-rotating vortex pairs
-
- Published online by Cambridge University Press:
- 22 September 2023, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Wind-tunnel measurements of sensible turbulent heat fluxes over melting ice
-
- Published online by Cambridge University Press:
- 25 October 2023, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Departure from the statistical equilibrium of large scales in forced three-dimensional homogeneous isotropic turbulence
-
- Published online by Cambridge University Press:
- 12 April 2024, A71
-
- Article
- Export citation
- Cited by 2
Numerical study of turbulent bubbly upflow: effect of density ratio
-
- Published online by Cambridge University Press:
- 17 March 2025, A63
-
- Article
- Export citation
- Cited by 2
Vortex structures under dimples and scars in turbulent free-surface flows
-
- Published online by Cambridge University Press:
- 17 March 2025, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Side-heated Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 13 November 2024, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Bubble-laden thermals in supersaturated water
-
- Published online by Cambridge University Press:
- 17 August 2021, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
A spatially accelerating turbulent flow with longitudinally contracting walls
-
- Published online by Cambridge University Press:
- 21 July 2022, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Graph theoretic methods for assessing the effects of a background shear current on internal solitary waves
-
- Published online by Cambridge University Press:
- 14 October 2024, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation