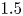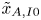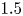Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2
Path instabilities of freely falling oblong cylinders
-
- Published online by Cambridge University Press:
- 27 November 2024, A54
-
- Article
- Export citation
- Cited by 2
Over-reflection of acoustic waves by supersonic exponential boundary layer flows
-
- Published online by Cambridge University Press:
- 13 July 2022, A9
-
- Article
- Export citation
- Cited by 2
Rayleigh–Taylor unstable condensing liquid layers with nonlinear effects of interfacial convection and diffusion of vapour
-
- Published online by Cambridge University Press:
- 06 October 2020, A1
-
- Article
- Export citation
- Cited by 2
How interfacial tension enhances drag in turbulent Taylor–Couette flow with neutrally buoyant and equally viscous droplets
-
- Published online by Cambridge University Press:
- 23 December 2024, A2
-
- Article
- Export citation
- Cited by 2
Understanding the effect of Prandtl number on momentum and scalar mixing rates in neutral and stably stratified flows using gradient field dynamics
-
- Published online by Cambridge University Press:
- 27 August 2024, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Single and multi-row turbine performance in bounded shear flow
-
- Published online by Cambridge University Press:
- 15 February 2023, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
The drag of a filament moving in a supported spherical bilayer
-
- Published online by Cambridge University Press:
- 10 January 2024, A6
-
- Article
- Export citation
- Cited by 2
Force and torque reactions on a pitching flexible aerofoil
-
- Published online by Cambridge University Press:
- 24 April 2023, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Buckled elastic sheet as a vortex generator in dual channels
-
- Published online by Cambridge University Press:
- 29 April 2024, A39
-
- Article
- Export citation
- Cited by 2
Spiral flow instability between a rotor and a stator in high-speed turbomachinery and its relation to fan noise
-
- Published online by Cambridge University Press:
- 26 June 2023, A1
-
- Article
- Export citation
- Cited by 2
Polymer and surfactant flows through a periodically constricted tube
-
- Published online by Cambridge University Press:
- 31 March 2023, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
The open channel in a uniform representation of the turbulent velocity profile across all parallel geometries
-
- Published online by Cambridge University Press:
- 25 January 2024, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Spatio-temporal dynamics of a two-layer pressure-driven flow subjected to a wall-normal temperature gradient
-
- Published online by Cambridge University Press:
- 15 February 2023, A11
-
- Article
- Export citation
- Cited by 2
Effect of wall suction on rotating disk absolute instability
-
- Published online by Cambridge University Press:
- 24 February 2016, pp. 704-737
-
- Article
- Export citation
- Cited by 2
The fluid mechanics of active flow control at very large scales
-
- Published online by Cambridge University Press:
- 22 November 2024, F9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Non-normality and small-scale statistics in a three-dimensional, separated shear flow
-
- Published online by Cambridge University Press:
- 09 May 2025, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Non-Oberbeck–Boussinesq effects on the linear stability of a vertical natural convection boundary layer
-
- Published online by Cambridge University Press:
- 24 July 2024, A44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Optimal unstirred state of a passive scalar
-
- Published online by Cambridge University Press:
- 28 January 2021, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
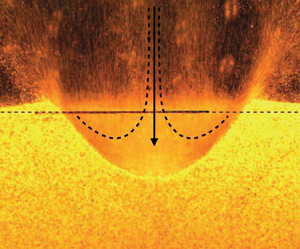
Air-jet impact craters on granular surfaces: a universal scaling
-
- Published online by Cambridge University Press:
- 30 October 2024, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Lift reversal for an oblate droplet translating in a linear shear flow: from inviscid bubble to rigid spheroid
-
- Published online by Cambridge University Press:
- 20 March 2025, A78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation