Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2
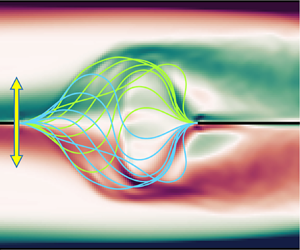
Buckled elastic sheet as a vortex generator in dual channels
-
- Published online by Cambridge University Press:
- 29 April 2024, A39
-
- Article
- Export citation
- Cited by 2
Lateral migration and bouncing of a deformable bubble rising near a vertical wall. Part 2. Highly inertial regimes
-
- Published online by Cambridge University Press:
- 18 June 2025, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Frequency selection in a gravitationally stretched capillary jet in the jetting regime
-
- Published online by Cambridge University Press:
- 29 April 2020, A6
-
- Article
- Export citation
- Cited by 2
Understanding the effect of Prandtl number on momentum and scalar mixing rates in neutral and stably stratified flows using gradient field dynamics
-
- Published online by Cambridge University Press:
- 27 August 2024, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
The drag of a filament moving in a supported spherical bilayer
-
- Published online by Cambridge University Press:
- 10 January 2024, A6
-
- Article
- Export citation
- Cited by 2
The effect of a non-linear basic temperature profile on the forced flow of a viscous liquid non-uniformly heated from below
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 385-397
-
- Article
- Export citation
- Cited by 2
Streaming of fluid under a near-bottom membrane
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 385-392
-
- Article
- Export citation
- Cited by 2
A note on nonlinear acoustic resonances in rectangular cavities
-
- Published online by Cambridge University Press:
- 12 April 2006, pp. 299-303
-
- Article
- Export citation
- Cited by 2
Wilson Cloud formation by low-altitude nuclear explosions
-
- Published online by Cambridge University Press:
- 12 April 2006, pp. 787-794
-
- Article
- Export citation
- Cited by 2
The nonlinear evolution of a slowly growing wave on a laterally sheared baroclinic flow
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 615-643
-
- Article
- Export citation
- Cited by 2
Minimizing shoreline pollution in rivers with tributaries
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 589-597
-
- Article
- Export citation
- Cited by 2
Waves generated in rotating fluids by travelling forcing effects
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 129-158
-
- Article
- Export citation
- Cited by 2
Cours de Mécanique des Milieux Continus. Tome 1.Théorie générale. By P. GERMAIN. Masson et Cie, 1973. 417 pp.
-
- Published online by Cambridge University Press:
- 29 March 2006, p. 191
-
- Article
- Export citation
- Cited by 2
On unsymmetrically impinging jets
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 653-655
-
- Article
- Export citation
- Cited by 2
Laminar and transitional flow of drilling muds and various suspensions in circular tubes
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 449-464
-
- Article
- Export citation
- Cited by 2
Unsteady boundary layers close to the stagnation region of slender bodies
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 315-332
-
- Article
- Export citation
- Cited by 2
Corrigendum: Stretched vortices – the sinews of turbulence; large-Reynolds-number asymptotics
-
- Published online by Cambridge University Press:
- 26 April 2006, p. 371
-
- Article
- Export citation
- Cited by 2
Hypersonic non-equilibrium flow over slender bodies
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 417-431
-
- Article
- Export citation
- Cited by 2
On the 3-D inverse potential target pressure problem. Part 2. Numerical aspects and application to duct design
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 147-162
-
- Article
- Export citation
- Cited by 2
Workbook on the Dispersion of Dense Gases. By R. E. BRITTER and J. MCQUAID. Health & Safety Executive, 1988. 128 pp. £35.
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 656-657
-
- Article
- Export citation