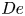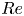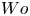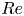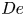Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
The effect of a sudden density change on a slightly non-uniform flow
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 385-399
-
- Article
- Export citation
- Cited by 1
Statistical Fluid Mechanics: The Mechanics of Turbulence, volume 1. By A. S. MONIN and A. M. YAGLOM. M. I. T. Press, 1971. 769 pp. £10.50.
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 410-414
-
- Article
- Export citation
- Cited by 1
A note on the application of the supersonic area rule to the determination of the wave drag of rectangular wings
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 575-582
-
- Article
- Export citation
- Cited by 1
A ray theory for wave propagation in a non-uniform medium
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 343-356
-
- Article
- Export citation
- Cited by 1
Ubungen zur Gasdynamik. By K. OSWATITSCH and R. SCHWARZENBERGER. Wien: Springer-Verlag, 1963. 180 pp. DM. 33.20
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 636-637
-
- Article
- Export citation
- Cited by 1
Resonant oscillations in radiative magnetogasdynamics
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 73-84
-
- Article
- Export citation
- Cited by 1
Low Reynolds Number Hydrodynamics. By J. HAPPEL & HOWARD BRENNER. Prentice-Hall, 1965. 553 pp. £6.
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 826-828
-
- Article
- Export citation
- Cited by 1
The decay of perturbations in an electrically conducting and thermally radiating gas
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 63-79
-
- Article
- Export citation
- Cited by 1
Resolvent analysis of turbulent flow laden with low-inertia particles
-
- Published online by Cambridge University Press:
- 23 April 2024, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Control of roughness-induced transition in supersonic flows by local wall heating strips
-
- Published online by Cambridge University Press:
- 12 November 2024, A16
-
- Article
- Export citation
- Cited by 1
Acoustic near field of a contra-rotating propeller in wetted conditions
-
- Published online by Cambridge University Press:
- 18 March 2025, A70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
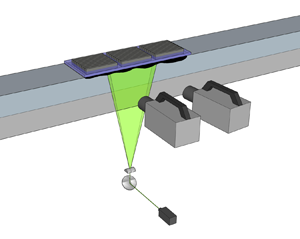
Hydrodynamic interactions between a sedimenting squirmer and a planar wall
-
- Published online by Cambridge University Press:
- 09 May 2025, A24
-
- Article
- Export citation
- Cited by 1
High-speed impacts of slender bodies into non-smooth, complex fluids
-
- Published online by Cambridge University Press:
- 19 December 2018, R1
-
- Article
- Export citation
- Cited by 1
Numerical study of the supersonic impinging jet oscillation and tone generation mechanism
-
- Published online by Cambridge University Press:
- 17 March 2025, A58
-
- Article
- Export citation
- Cited by 1
Asymptotic matching modal model on Richtmyer–Meshkov instability
-
- Published online by Cambridge University Press:
- 26 December 2024, A16
-
- Article
- Export citation
- Cited by 1
Toward coherently representing turbulent wall-flow dynamics
-
- Published online by Cambridge University Press:
- 01 October 2013, pp. 1-4
-
- Article
-
- You have access
- Export citation
- Cited by 1
Computational Fluid Mechanics and Heat Transfer. By D. A ANDERSON, J. C. TANNEHILL and R. H. PLETCHER. Hemisphere, 1984. 599 pp. $39.95.
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 564-565
-
- Article
- Export citation
- Cited by 1
Fluid dynamics in intracranial aneurysms treated with flow-diverting stents: effect of multiple geometrical parameters
-
- Published online by Cambridge University Press:
- 23 October 2023, A45
-
- Article
- Export citation
- Cited by 1
Drag reduction utilizing a wall-attached ferrofluid film in turbulent channel flow
-
- Published online by Cambridge University Press:
- 02 October 2024, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
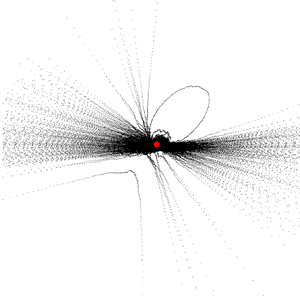
Caustics in turbulent aerosols: an excitable system approach
-
- Published online by Cambridge University Press:
- 30 September 2022, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation