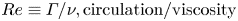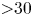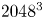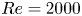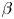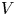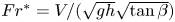Open access
Contents
JFM Papers
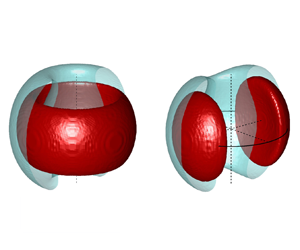
Helicity dynamics in viscous vortex links
-
- Published online by Cambridge University Press:
- 05 July 2022, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
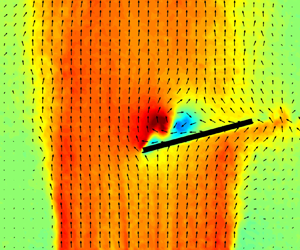
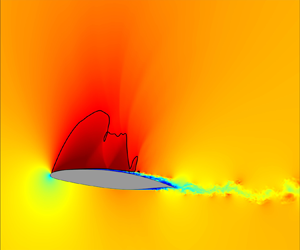
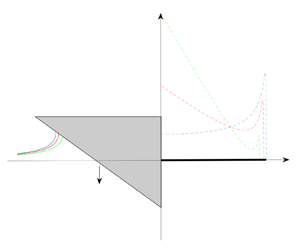
Experimental characterization of smooth body flow separation topography and topology on a two-dimensional geometry of finite span
-
- Published online by Cambridge University Press:
- 05 July 2022, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the interaction of turbulence with nucleation and growth in reaction crystallisation
-
- Published online by Cambridge University Press:
- 05 July 2022, A48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diffraction of shock waves through a non-quiescent medium
-
- Published online by Cambridge University Press:
- 04 July 2022, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint reconstruction and segmentation of noisy velocity images as an inverse Navier–Stokes problem
-
- Published online by Cambridge University Press:
- 04 July 2022, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Physics of gust response mitigation in open-loop pitching manoeuvres
-
- Published online by Cambridge University Press:
- 01 July 2022, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reynolds number dependence of Lagrangian dispersion in direct numerical simulations of anisotropic magnetohydrodynamic turbulence
-
- Published online by Cambridge University Press:
- 01 July 2022, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Onset of nonlinearity in oscillatory flow through a hexagonal sphere pack
-
- Published online by Cambridge University Press:
- 30 June 2022, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Speaker-wire vortices in stratified anabatic Prandtl slope flows and their secondary instabilities
-
- Published online by Cambridge University Press:
- 30 June 2022, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thermotaxis of a deformable droplet in a confined Poiseuille flow
-
- Published online by Cambridge University Press:
- 29 June 2022, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
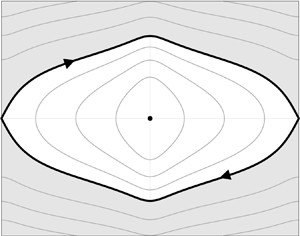
Quasi-equilibrium states for helical vortices with swirl
-
- Published online by Cambridge University Press:
- 29 June 2022, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
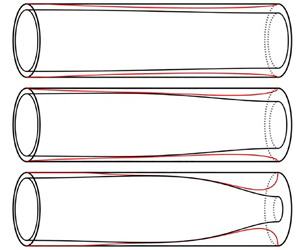
Surface-tension-driven evolution of a viscoplastic liquid coating the interior of a cylindrical tube
-
- Published online by Cambridge University Press:
- 28 June 2022, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamic performance of oscillating elastic propulsors with tapered thickness
-
- Published online by Cambridge University Press:
- 28 June 2022, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large-eddy simulations and modal reconstruction of laminar transonic buffet
-
- Published online by Cambridge University Press:
- 27 June 2022, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Microscopic pumping of viscous liquids with single cavitation bubbles
-
- Published online by Cambridge University Press:
- 27 June 2022, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gravity effects in two-dimensional and axisymmetric water impact models
-
- Published online by Cambridge University Press:
- 24 June 2022, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spontaneous and explicit symmetry breaking of thermoacoustic eigenmodes in imperfect annular geometries
-
- Published online by Cambridge University Press:
- 24 June 2022, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Emergent rheotaxis of shape-changing swimmers in Poiseuille flow
-
- Published online by Cambridge University Press:
- 24 June 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Attenuation of the unsteady loading on a high-rise building using feedback control
-
- Published online by Cambridge University Press:
- 24 June 2022, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure and dynamics of a laminar separation bubble near a wing root: towards reconstructing the complete LSB topology on a finite wing
-
- Published online by Cambridge University Press:
- 24 June 2022, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation