We numerically investigate the mechanism resulting in fate change of a hydrophobic sphere impacting onto a confined pool, that is, at the same impact speed, it does not submerge in a wide pool but does in a narrow pool. We find that the reflection of the impact-induced gravity-capillary waves from the pool boundary is responsible for this phenomenon. In particular, the return of the wave to the symmetry axis may coincide with the rising of the impacting sphere to the water surface, which corresponds to the critical conditions of the fate change. Moreover, for the spheres at the onset of submersion in a wide pool, our analysis suggests that this scenario also accounts for an interesting observation in the numerical simulations. That is, the effective pool size $S_{c}$, beyond which the submersion of impacting spheres is no longer affected by the pool size $S$, is mainly dependent on the sphere diameter, no matter whether the surface waves are the capillary or gravity waves. For $S<S_{c}$, two important pool sizes ($S_{w,1}$ and $S_{w,2}$, and $S_{w,2}\geqslant S_{w,1}$) are identified at the same impact speed, and the sphere submersion takes place at $S_{w,1}\leqslant S\leqslant S_{w,2}$. Based on the flow features identified in simulations, a scaling law is proposed to correlate the Weber number and Bond number with $S_{w}$. The theoretical prediction is shown to agree well with the numerical results.

Relaxation of a colloidal dispersion following flow shutoff occurs over distinct time scales, providing a useful method for identifying microscopic forces that are otherwise difficult to detect. Active microrheology facilitates such interrogation for small-scale systems such as biological cells, where a Brownian probe is driven by an external force through the dispersion and its motion is tracked to infer flow properties. An interplay between external forces, Brownian motion, hydrodynamic interactions and interparticle forces deforms the microstructure surrounding the probe, which alters probe speed. Application of the Stokes drag law relates mean probe speed to the effective viscosity of the embedding medium. We present a micromechanical theoretical model for this relationship during nonlinear transient relaxation upon removal of the external force. Upon cessation, contributions to viscosity linear in the force vanish instantly, but hydrodynamics influences subsequent relaxation, as well as the pre-cessation structure that sets the initial condition. Stronger pre-cessation flow drives faster relaxation of both structure and rheology. Non-equilibrium entropic contributions persist after shutoff, decaying over time. Hydrodynamic interactions slow this relaxation by hindering relative Brownian and interparticle displacements. The dissipation of entropically stored energy produces a deterministic force that drives deterministic probe motion even after the external force is removed, giving a natural connection to the chemical potential. Using this idea, we show that probe back-travel gives a direct measure of the osmotic pressure and the time scale over which entropically stored energy is dissipated. Modelling a range of repulsions provides a platform for particle formulation tuned to desired transient response.

Current understanding of turbulence modulation by solid particles is incomplete as making reliable predictions on the nature and level of modulation remains a challenging task. Multiple modulation mechanisms may be simultaneously induced by particles, but the lack of reliable methods to identify these mechanisms and quantify their effects hinders a complete understanding of turbulence modulation. In this work, we present a full analysis of the turbulent kinetic energy (TKE) equation for a turbulent channel flow laden with a few fixed particles near the channel walls, in order to investigate how the wall generated turbulence interacts with the particles and how, as a result, the global turbulence statistics are modified. All terms in the budget equations of total and component-wise TKEs are explicitly computed using the data from direct numerical simulations. Particles are found to modify turbulence by two competing mechanisms: the reduction of the intrinsic turbulence production associated with a reduced mean shear due to the resistance imposed by solid particles (the first mechanism), and an additional TKE production mechanism by displacing incoming fluid (the second mechanism). The distribution of TKE in the wall-normal direction is also made more homogeneous due to the significantly enhanced pressure transport of TKE. Finally, the budget analysis of component-wise TKE reveals an enhanced inter-component TKE transfer due to the presence of particles, which leads to a more isotropic distribution of TKE among three velocity components.

We investigate the stability of radial viscous fingering (VF) in miscible fluids. We show that the instability is determined by an interplay between advection and diffusion during the initial stages of flow. Using linear stability analysis and nonlinear simulations, we demonstrate that this competition is a function of the radius $r_{0}$ of the circular region initially occupied by the less-viscous fluid in the porous medium. For each $r_{0}$, we further determine the stability in terms of Péclet number ($Pe$) and log-mobility ratio ($M$). The $Pe{-}M$ parameter space is divided into stable and unstable zones: the boundary between the two zones is well approximated by $M_{c}=\unicode[STIX]{x1D6FC}(r_{0})Pe_{c}^{-0.55}$. In the unstable zone, the instability is reduced with an increase in $r_{0}$. Thus, a natural control measure for miscible radial VF in terms of $r_{0}$ is established. Finally, the results are validated by performing experiments that provide good qualitative agreement with our numerical study. Implications for observations in oil recovery and other fingering instabilities are discussed.

A bubble injected into a flow rotating about a horizontal axis comes to an equilibrium location. The drag and lift exerted on the bubble can be measured and the bubble wake visualized (Rastello et al., J. Fluid Mech., vol. 624, 2009, pp. 159–178; Rastello et al., J. Fluid Mech., vol. 682, 2011, pp. 434–459; Rastello et al.,J. Fluid Mech., vol. 831, 2017, pp. 529–617). For a contaminated bubble, interface deformation remains limited. The bubble is freely rotating, which results in a complex separated wake, influenced by rotational flow and bubble spinning. The wake is described by analysing the near- and far-wake geometry and behaviour from laser-sheet visualizations, as a function of the relevant non-dimensional numbers: bubble Reynolds number 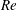$Re$, Rossby number 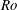$Ro$, and non-dimensional spinning rate 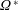$\unicode[STIX]{x1D6FA}^{\ast }$. As the far-wake length increases with 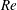$Re$, it deflects towards the rotation axis of the flow, the deflection angle increasing with 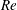$Re$ and being twice the angle that would occur without deflection. Deflection is stronger for bubbles located close to the rotation axis of the flow (small 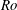$Ro$). The far wake is more curved than the incoming streamlines. The near wake exhibits three distinct regimes as a function of 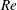$Re$. For 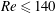$Re\leqslant 140$, the near wake is structured by the bubble spinning. Its size is related to 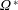$\unicode[STIX]{x1D6FA}^{\ast }$ and grows faster with 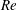$Re$ than for a stationary sphere in a uniform flow. As the bubble spinning is saturating (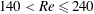$140<Re\leqslant 240$), these differences vanish and 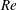$Re$ dependences for the two situations becomes comparable. For 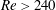$Re>240$, wake instability generates a bubble precession that makes the near wake decrease rapidly for higher 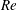$Re$. These regimes coincide with the changes in the lift coefficients that we have noted in our studies.

Inclined turbulent thermal convection in liquid sodium is studied at large Rayleigh numbers $Ra\gtrsim 10^{7}$ based on the results of both experimental measurements and high-resolution numerical simulations. For a direct comparison, the considered system parameters are set to be similar: $Ra=1.67\times 10^{7}$ in the direct numerical simulations (DNS), $Ra=1.5\times 10^{7}$ in the large-eddy simulations and $Ra=1.42\times 10^{7}$ in the experiments, while the Prandtl number of liquid sodium is very small ($Pr\approx 0.009$). The cylindrical convection cell has an aspect ratio of one; one circular surface is heated, while the other one is cooled. Additionally, the cylinder is inclined with respect to gravity and the inclination angle varies from $\unicode[STIX]{x1D6FD}=0^{\circ }$, which corresponds to Rayleigh–Bénard convection (RBC), to $\unicode[STIX]{x1D6FD}=90^{\circ }$, as in a vertical convection (VC) set-up. Our study demonstrates quantitative agreement of the experimental and numerical results, in particular with respect to the global heat and momentum transport, temperature and velocity profiles, as well as the dynamics of the large-scale circulation (LSC). The DNS reveal that the twisting and sloshing of the LSC at small inclination angles periodically affects the instantaneous heat transport (up to $\pm 44\,\%$ of the mean heat transport). The twisted LSC is associated with a weak heat transport, while the sloshing mode that brings together the hot and cold streams of the LSC is associated with a strong heat transport. The experiments show that the heat transport scales as $Nu\sim Ra^{0.22}$ in both limiting cases (RBC and VC) for Rayleigh numbers around $Ra\approx 10^{7}$, while any inclination of the cell, $0<\unicode[STIX]{x1D6FD}\leqslant 90^{\circ }$, leads to an increase of $Nu$.

Moist Rayleigh–Bénard convection with water saturated boundaries is explored using a One-Dimensional Turbulence model. The system involves both temperature $T$ and water vapour pressure $e_{v}$ as driving scalars. The emphasis of the work is on a supersaturation $s$, a nonlinear combination of $T$ and $e_{v}$ that is crucial to cloud formation. Its mean as well as fluctuation statistics determine cloud droplet growth and therefore precipitation formation and cloud optical properties. To explore the role of relative scalar diffusivities for temperature ($D_{t}$) and water vapour ($D_{v}$), three different regimes are considered: $D_{v}>D_{t}$, $D_{v}\approx D_{t}$ and $D_{v}<D_{t}$. Scalar fluxes (Nusselt number, $Nu$ and Sherwood number, $Sh$) and their scalings with moist Rayleigh number $Ra_{moist}$ are consistent with previous studies of one-component convection. Moreover, variances of the scalars in the bulk region increase with their diffusivities and also reasonably follow derived scaling expressions. Eulerian properties plotted in $(T,e_{v})$ coordinates have a different slope compared to an idealized mixing process. Additionally, the scalars are highly correlated, even in the cases of high relative diffusivities (factor of four) $D_{v}$ and $D_{t}$. Based on the above fact and the scaling relation of the scalars, the supersaturation variance is found to vary approximately as $Ra_{moist}^{5/3}$, in agreement with numerical results. Finally, the supersaturation profile in the boundary layer is explored and compares well with scalar boundary layer models. A sharp peak appears in the boundary-layer-supersaturation profile, not only in the variance but also in the mean profile, due to relative diffusivities of the scalars.

We report an experimental study of the reconstruction of real-ocean rogue waves in a laboratory environment using the time reversal (TR) methodology (Chabchoub & Fink, Phys. Rev. Lett., vol. 112, 2014, 124101). Three different rogue wave measurements are used to validate the TR approach. The generation and accurate control of target free-surface profiles in a unidirectional wave flume using standard techniques, such as the New Wave theory (Tromans, Anaturk & Hagemeier, Proceedings of the First International Offshore and Polar Engineering Conference, 1991, pp. 64–71), are fairly challenging, especially for very steep and, thus, highly nonlinear extreme waves. The TR method, making use of the time reversibility of wave propagation and symmetry of the governing hydrodynamic equations of motion, leads to a simple two-step experimental procedure, the accuracy of which is investigated in this paper. The use of the TR procedure requires the appropriate Froude scaling in designing the model-scale experiments. The present study represents the first validation of the TR method to realistic irregular seas containing rogue waves. Three extreme wave profiles are tested to assess the applicability of the TR scheme to different wave configurations taking into account variable characteristics. This includes the famed New Year wave. The accuracy of the TR method is demonstrated with varying wave steepness values and propagation distances of the reverse reconstruction. It is demonstrated that the unidirectional TR reconstruction is robust, even in the presence of unavoidable wave breaking, known to be an irreversible process within the framework of any wave hydrodynamic evolution equation, and independently of complex environmental conditions or focusing mechanism at play in the sea.

The surface texture of materials plays a critical role in wettability, turbulence and transport phenomena. In order to design surfaces for these applications, it is desirable to characterise non-smooth and porous materials by their ability to exchange mass and momentum with flowing fluids. While the underlying physics of the tangential (slip) velocity at a fluid–solid interface is well understood, the importance and treatment of normal (transpiration) velocity and normal stress is unclear. We show that, when the slip velocity varies at an interface above the texture, a non-zero transpiration velocity arises from mass conservation. The ability of a given surface texture to accommodate a normal velocity of this kind is quantified by a transpiration length. We further demonstrate that normal momentum transfer gives rise to a pressure jump. For a porous material, the pressure jump can be characterised by so-called resistance coefficients. By solving five Stokes problems, the introduced measures of slip, transpiration and resistance can be determined for any anisotropic non-smooth surface consisting of regularly repeating geometric patterns. The proposed conditions are a subset of the effective boundary conditions derived from formal multi-scale expansion. We validate and demonstrate the physical significance of the effective conditions on two canonical problems – a lid-driven cavity and a turbulent channel flow, both with non-smooth bottom surfaces.

The incompressible two-dimensional Euler equations on a sphere constitute a fundamental model in hydrodynamics. The long-time behaviour of solutions is largely unknown; statistical mechanics predicts a steady vorticity configuration, but detailed numerical results in the literature contradict this theory, yielding instead persistent unsteadiness. Such numerical results were obtained using artificial hyperviscosity to account for the cascade of enstrophy into smaller scales. Hyperviscosity, however, destroys the underlying geometry of the phase flow (such as conservation of Casimir functions), and therefore might affect the qualitative long-time behaviour. Here, we develop an efficient numerical method for long-time simulations that preserve the geometric features of the exact flow, in particular conservation of Casimirs. Long-time simulations on a non-rotating sphere then reveal three possible outcomes for generic initial conditions: the formation of either 2, 3 or 4 coherent vortex structures. These numerical results contradict the statistical mechanics theory and show that previous numerical results, suggesting 4 coherent vortex structures as the generic behaviour, display only a special case. Through integrability theory for point vortex dynamics on the sphere we present a theoretical model which describes the mechanism by which the three observed regimes appear. We show that there is a correlation between a first integral $\unicode[STIX]{x1D6FE}$ (the ratio of total angular momentum and the square root of enstrophy) and the long-time behaviour: $\unicode[STIX]{x1D6FE}$ small, intermediate and large yields most likely 4, 3 or 2 coherent vortex formations. Our findings thus suggest that the likely long-time behaviour can be predicted from the first integral $\unicode[STIX]{x1D6FE}$.

The dynamics of bubbles near infinite boundaries has been studied in great detail. Once viscosity is accounted for, large wall shear stresses are generated upon jet impact and spreading. Although earlier works covered bubble dynamics in thin gaps and revealed rich fluid dynamics, viscosity and the resulting mechanical action on the surface have not been addressed. Here, we report experimental and numerical studies of cavitation bubbles expanding and collapsing inside a narrow gap. High-speed recordings and numerical simulations demonstrate an unexpected enhancement of the jetting velocity, a centre of mass translation and a dramatic increase of the wall shear stress. For the latter, we use computational simulations and present the results as spatio-temporal shear stress maps, while the bubble is recorded with high-speed photography. To test the implications of the high wall shear stress combined with the bubble translation, we conducted two experimental demonstrations. The first shows particulate removal on the distant wall, and the second cell detachment and molecule delivery through the cell membrane.

Natural swimmers rely for their survival on sensors that gather information from the environment and guide their actions. The spatial organization of these sensors, such as the visual fish system and lateral line, suggests evolutionary selection, but their optimality remains an open question. Here, we identify sensor configurations that enable swimmers to maximize the information gathered from their surrounding flow field. We examine two-dimensional, self-propelled and stationary swimmers that are exposed to disturbances generated by oscillating, rotating and D-shaped cylinders. We combine simulations of the Navier–Stokes equations with Bayesian experimental design to determine the optimal arrangements of shear and pressure sensors that best identify the locations of the disturbance-generating sources. We find a marked tendency for shear stress sensors to be located in the head and the tail of the swimmer, while they are absent from the midsection. In turn, we find a high density of pressure sensors in the head along with a uniform distribution along the entire body. The resulting optimal sensor arrangements resemble neuromast distributions observed in fish and provide evidence for optimality in sensor distribution for natural swimmers.

The characteristics and dynamics of the uniform-momentum zones (UMZ) and UMZ interfaces in a fully developed turbulent pipe flow are studied using direct numerical simulation at $Re_{\unicode[STIX]{x1D70F}}=500$. The multiple UMZs detected from the probability density functions of the instantaneous streamwise velocity following de Silva et al. (J. Fluid Mech., vol. 786, 2016, pp. 309–331) showed similarities to both turbulent channel and boundary layer flows (TBL): the hierarchical structural distribution of thinner UMZs with thinner interfaces nearer the wall, accompanied with sharper and larger jumps in the streamwise velocity at the UMZ interface. The conditional average results indicate that channel and pipe are very similar quantitatively whereas pipe and TBL display significant discrepancies. The innermost UMZs in pipe flow exhibit different behaviours to the other UMZs in pipes. The contortion of the UMZ interface representing the meandering of coherent motions with high- and low-momentum streaks is examined three-dimensionally. The meandering of UMZ in both two and three dimensions intensifies away from the wall and is always wavier in the azimuthal direction than the streamwise direction. The UMZs in the near-wall region capture the small-scale velocity fluctuation of the near-wall cycle and show asymmetric modulation of $Q2$ ejections over $Q4$ sweeps. The asymmetric modulation of ejections over sweeps decreases from the wall towards the pipe centre and the opposite trend of elevated $Q4$ sweeps is observed for the innermost UMZs. Near the wall, the ejection regions are very spiky compared to the flat sweep regions whereas, in the pipe centre, the large-scale ejections are relatively flat and the sweep regions are spikier.

We perform direct numerical simulations of rotating turbulent Waleffe flow, the flow between two parallel plates with a sinusoidal streamwise shear driving force, to study the formation of large-scale structures and the mechanisms for momentum transport. We simulate different cyclonic and anticyclonic rotations in the range of dimensionless rotation numbers (inverse Rossby numbers) $R_{\unicode[STIX]{x1D6FA}}\in [-0.16,2.21]$, and fix the Reynolds number to $Re=3.16\times 10^{3}$, large enough such that the shear transport is almost entirely due to Reynolds stresses and viscous transport is negligible. We find an optimum rotation in the anticyclonic regime at $R_{\unicode[STIX]{x1D6FA}}=0.63$, where a given streamwise momentum transport in the wall-normal direction is achieved with minimum mean energy of the streamwise flow. We link this optimal transport to the strength of large-scale structures, as was done in plane Couette flow by Brauckmann & Eckhardt (J. Fluid Mech., vol. 815, 2017, pp. 149–168). Furthermore, we explore the large-scale structures and their behaviour under spanwise rotation, and find disorganized large structures at $R_{\unicode[STIX]{x1D6FA}}=0$ but highly organized structures in the anticyclonic regime, similar to the rolls in rotating plane Couette and turbulent Taylor–Couette flow. We compare the large-scale structures of plane Couette flow and Waleffe flow, and observe that the streamwise vorticity is localized inside the cores of the rolls. We show that the rolls take energy from the mean flow at long time scales, and relate these structures to eigenvalues of the streamfunction.

The regular reflection to Mach reflection ($\text{RR}\rightarrow \text{MR}$) transition in inviscid perfect air for shock reflection over convex and straight wedges is investigated. Provided that the variation of shock intensity only has a second-order effect on the wave transition, the possible cases for the occurrence of the $\text{RR}\rightarrow \text{MR}$ transition for curved shock reflection over a wedge are discussed. For a planar shock reflecting over a convex wedge, four different flow regions are classified and the mechanism of the disturbance propagation is interpreted. It is found that the flow-induced rarefaction waves exist between disturbances generated from neighbouring positions and isolate them. For a curved shock reflecting over a convex wedge, although the distributions of the flow regions are different from those in planar shock reflection, the analysis for the planar shock case can be extended to curved shock cases as long as the wedge is convex. When a diverging shock reflects off a straight wedge, the flow-induced rarefaction waves are absent. However, the disturbances generated earlier cannot overtake the reflection point before the pseudo-steady criterion is satisfied. In the cases considered, the flow in the vicinity of the reflection point will not be influenced by the unsteady flow caused by the shock intensity and the wedge angle variations. This is clearly a local property of the shock–wall interaction, no matter what the history of the shock trajectory is. For validation, extensive inviscid numerical simulations are performed, and the numerical results show the reliability of the pseudo-steady criterion for predicting the $\text{RR}\rightarrow \text{MR}$ transition on a convex wedge.

We study numerically the region of convergence of the normal form transformation for the case of the Charney–Hasagawa–Mima (CHM) equation to investigate whether certain finite amplitude effects can be described in normal form coordinates. Specifically, we consider a Galerkin truncation of the CHM equation to four Fourier modes, and ask: Can the finite amplitude phenomenon known as precession resonance (Bustamante et al., Phys. Rev. Lett., vol. 113, 2014, 084502) be described by the normal form variables of wave turbulence theory? The answer is no, due to the failure of convergence of the normal form transformation at the wave amplitudes required for precession resonance. We show this by first characterising precession resonance in the original system, then, searching for this resonance in the normal form equations of motion. We find a large discrepancy between the dynamics of the original system and the transformed normal form system. This prompts an investigation into the convergence of the transformation in the state space of wave amplitudes. We find that the numerically calculated region of convergence is a region of finite wave amplitudes, well beyond the usual limit of weak nonlinearity. However, the amplitudes at the boundary of this region of convergence (i.e. the amplitudes at which the normal form transformation begins to diverge) match closely with the amplitudes at which precession resonance occurs in the original system. We conclude that the precession resonance mechanism cannot be explained by the usual methods of normal forms in wave turbulence theory, so a more general theory for intermediate nonlinearity is required.

We study the emergence of precessing vortex core (PVC) oscillations in a swirling jet experiment. We vary the swirl intensity while keeping the net mass flow rate fixed using a radial-entry swirler with movable blades upstream of the jet exit. The swirl intensity is quantified in terms of a swirl number $S$. Time-resolved velocity measurements in a radial–axial plane anchored at the jet exit for various $S$ values are obtained using stereoscopic particle image velocimetry. Spectral proper orthogonal decomposition and spatial cross-spectral analysis reveal the simultaneous emergence of a bubble-type vortex breakdown and a strong helical limit-cycle oscillation in the flow for $S>S_{c}$ where $S_{c}=0.61$. The oscillation frequency, $f_{PVC}$, and the square of the flow oscillation amplitudes vary linearly with $S-S_{c}$. A solution for the coherent unsteady field accurate up to $O(\unicode[STIX]{x1D716}^{3})$ ($\unicode[STIX]{x1D716}\sim O((S-S_{c})^{1/2})$) is determined from the nonlinear Navier–Stokes equations, using the method of multiple scales. We show that onset of bubble type vortex breakdown at $S_{c}$, results in a marginally stable, helical linear global hydrodynamic mode. This results in the stable limit-cycle precession of the breakdown bubble. The variation of $f_{LC}$ with $S-S_{c}$ is determined from the Stuart–Landau equation associated with the PVC. Reasonable agreement with the corresponding experimental result is observed, despite the highly turbulent nature of the flow in the present experiment. Further, amplitude saturation results from the time-averaged distortion imposed on the flow by the PVC, suggesting that linear stability analysis may predict PVC characteristics for $S>S_{c}$.

A small-disturbance asymptotic model is derived to describe the complex nature of a pure water vapour flow with non-equilibrium and homogeneous condensation around a thin airfoil operating at transonic speed and small angle of attack. The van der Waals equation of state provides real-gas relationships among the thermodynamic properties of water vapour. Classical nucleation and droplet growth theory is used to model the condensation process. The similarity parameters which determine the flow and condensation physics are identified. The flow may be described by a nonlinear and non-homogeneous partial differential equation coupled with a set of four ordinary differential equations to model the condensation process. The model problem is used to study the effects of independent variation of the upstream flow and thermodynamic conditions, airfoil geometry and angle of attack on the pressure and condensate mass fraction distributions along the airfoil surfaces and the consequent effect on the wave drag and lift coefficients. Increasing the upstream temperature at fixed values of upstream supersaturation ratio and Mach number results in increased condensation and higher wave drag coefficient. Increasing the upstream supersaturation ratio at fixed values of upstream temperature and Mach number also results in increased condensation and the wave drag coefficient increases nonlinearly. In addition, the effects of varying airfoil geometry with a fixed thickness ratio and chord on flow properties and condensation region are studied. The computed results confirm the similarity law of Zierep & Lin (Forsch. Ing. Wes. A, vol. 33 (6), 1967, pp. 169–172), relating the onset condensation Mach number to upstream stagnation relative humidity, when an effective specific heat ratio is used. The small-disturbance model is a useful tool to analyse the physics of high-speed condensing steam flows around airfoils operating at high pressures and temperatures.

Past experimental studies have indicated that the Rayleigh fission of a charged drop occurs via the formation of a jet followed by emission of progeny droplets. In order to understand this process, we model the evolution of a drop using an axisymmetric boundary element method in the viscous limit. In this work, the electrostatic model of a charged viscous liquid drop is modified by including surface charge dynamics. This model accounts for the finite charge relaxation time scales over which the drop surface is charged as well as the convection of charges by the interfacial flow. It is observed that, as the drop deforms with time, the generally applied assumption of an equipotential surface becomes invalid near the conical ends that experience singularly fast dynamics and the associated surface charge dynamics gives rise to tangential electric stresses. These tangential electric stresses exert an axial momentum on the fluid and are responsible for the formation of a jet and progeny droplets. Further, the progeny droplets are found to follow an inverse power-law scaling with the conductivity of the liquid and the smaller sized progenies carry a charge close to its Rayleigh limit.

The passive oscillations of inverted flags are investigated both experimentally and theoretically in this paper. First, the force and energy distributions of inverted flags, which contain elastic and inertia components, are analysed based on the experimental data. Two main differences between inverted and conventional flags are found: (1) the elastic energy of a conventional flag is concentrated near the free end, while the fixed end of an inverted flag presents the largest elastic energy; and (2) the elastic component is several orders of magnitude greater than the inertia component for an inverted flag, while they are of the same magnitude for a conventional flag. Second, a linear analysis shows that the critical flow velocities obtained from the experiments at small mass ratios are scattered around the theoretical curve of wavenumber $k=1.875$, which is in contrast with $k=4.694$ of a conventional flag. For large mass ratios, the mass ratio has a certain influence on the critical velocity rather than being irrelevant. For two parallel inverted flags, both the experimental and theoretical results indicate that the range of the in-phase flapping mode becomes smaller with an increase in the separation distance, and a multiple flapping state may occur. For $n\geqslant 2$ parallel inverted flags, the theoretical results show that two of all coupled flapping modes are dominant with most parameters. These findings could contribute to a better understanding of the passive oscillations of inverted flags.